昆明網(wǎng)站建設(shè)是什么意思福州seo技巧培訓(xùn)
文章目錄
- 母函數(shù)---解決計(jì)數(shù)
- 遞推關(guān)系
- 常系數(shù)線性齊次遞推關(guān)系
- 常系數(shù)線性非齊次遞推關(guān)系
- 漢諾塔遞推關(guān)系
母函數(shù)—解決計(jì)數(shù)
普母函數(shù)—組合問(wèn)題
指母函數(shù)—排列問(wèn)題

f(x)= ∑ i = 1 n a i x i = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + . . . + a n x n C n 0 + C n 1 ? x + C n 2 ? x 2 + . . . + C n n ? x n = \sum_{i=1}^n{a_ix^i}=\\ a_0 +a_1x + a_2 x^2 + a_3x^3+...+a_nx^n\\ C_n^0+C_n^1*x+C_n^2*x^2+...+C_n^n*x^n = ∑i=1n?ai?xi=a0?+a1?x+a2?x2+a3?x3+...+an?xnCn0?+Cn1??x+Cn2??x2+...+Cnn??xn= ( 1 + x ) n (1+x)^n (1+x)n
( 1 + x ) n = ∑ k = 0 n C n k x k = ∑ k = 0 n C n n ? k x k (1+x)^n = \sum_{k=0}^nC_n^kx^k=\sum_{k=0}^nC_n^{n-k}x^k (1+x)n=∑k=0n?Cnk?xk=∑k=0n?Cnn?k?xk

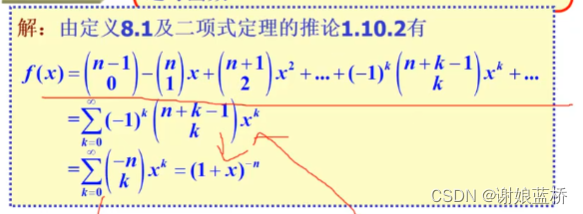
∑ k = 0 ∞ ( ? 1 ) k C n + k ? 1 k z k = 1 ( 1 + z ) n = ( 1 + z ) ? n \sum_{k=0}^\infty (-1)^kC_{n+k-1}^{k}z^k=\frac{1}{(1+z)^n}=(1+z)^{-n} ∑k=0∞?(?1)kCn+k?1k?zk=(1+z)n1?=(1+z)?n
( 1 + z ) α = ∑ k = 0 ∞ C α k z k (1+z)^{\alpha}=\sum_{k=0}^{\infty}C_{\alpha}^kz^k (1+z)α=∑k=0∞?Cαk?zk
( 1 ? z ) ? n = 1 ( 1 ? z ) ? n = ∑ k = 0 ∞ C n + k ? 1 k z k 其中 ∣ z ∣ < 1 (1-z)^{-n} = \frac{1}{(1-z)^{-n}}=\sum_{k=0}^{\infty}C_{n+k-1}^{k}z^k \quad 其中|z|<1 (1?z)?n=(1?z)?n1?=∑k=0∞?Cn+k?1k?zk其中∣z∣<1
∑ n = 1 ∞ C 2 n n x n = ( 1 ? 4 x ) ? 1 2 \sum_{n=1}^{\infty}C_{2n}^{n}x^n=(1-4x)^{-\frac{1}{2}} ∑n=1∞?C2nn?xn=(1?4x)?21?
其中 C 2 n n = 2 n ! n ! ? n ! = 2 n ? n ! n ! ? n ! = 2 n n ! 其中 C_{2n}^n=\frac{2n!}{n!*n!}=\frac{2^n*n!}{n!*n!}=\frac{2^n}{n!} 其中C2nn?=n!?n!2n!?=n!?n!2n?n!?=n!2n?
1 ( 1 + x ) = ∑ k = 0 ∞ C ? 1 k z k = ∑ k = 0 ∞ ( ? 1 ) k x k \frac {1}{(1+x)} = \sum_{k=0}^{\infty}C_{-1}^kz^k=\sum_{k=0}^{\infty}(-1)^kx^k (1+x)1?=∑k=0∞?C?1k?zk=∑k=0∞?(?1)kxk
1 1 ? x = ∑ n = 0 ∞ x n \frac {1}{1-x}=\sum_{n=0}^{\infty}x^n 1?x1?=∑n=0∞?xn
1 ( 1 ? x ) 2 = ∑ n = 0 ∞ ( n + 1 ) x n \frac{1}{(1-x)^2}=\sum_{n=0}^{\infty}(n+1)x^n (1?x)21?=∑n=0∞?(n+1)xn
2 ( 1 ? x ) 3 = ∑ n = 2 ∞ n ( n ? 1 ) x n ? 2 \frac{2}{(1-x)^3}=\sum_{n=2}^{\infty}n(n-1)x^{n-2} (1?x)32?=∑n=2∞?n(n?1)xn?2
6 ( 1 ? x ) 4 = ∑ n = 3 ∞ n ( n ? 1 ) ( n ? 2 ) x n ? 3 \frac{6}{(1-x)^4}=\sum_{n=3}^{\infty}n(n-1)(n-2)x^{n-3} (1?x)46?=∑n=3∞?n(n?1)(n?2)xn?3
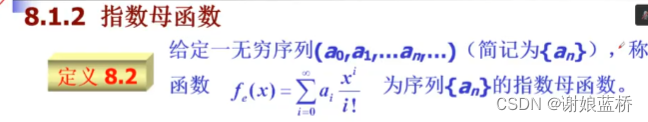
f ( x ) = a 0 + a 1 x 1 1 ! + a 2 x 2 2 ! + . . . + a n x n n ! f(x) = a_0 +a_1\frac{x_1}{1!}+a_{2}\frac{x^2}{2!}+...+a_{n}\frac{x^n}{n!} f(x)=a0?+a1?1!x1??+a2?2!x2?+...+an?n!xn?
e a x = 1 + a x 1 ! + a 2 x 2 2 ! + . . . + a n x n n ! + . . . e^{ax} = 1+a\frac{x}{1!}+a^2\frac{x^2}{2!}+...+a^n\frac{x^n}{n!}+... eax=1+a1!x?+a22!x2?+...+ann!xn?+...
e ? x = 1 ? x 1 ! + x 2 2 ! + . . . + ( ? 1 ) n x n n ! . . . e^{-x}=1-\frac{x}{1!}+\frac{x^2}{2!}+...+(-1)^n\frac{x^n}{n!}... e?x=1?1!x?+2!x2?+...+(?1)nn!xn?...
e x = 1 + x 1 ! + x 2 2 ! + . . . + x n n ! . . . e^{x}=1+\frac{x}{1!}+\frac{x^2}{2!}+...+\frac{x^n}{n!}... ex=1+1!x?+2!x2?+...+n!xn?...
s i n ( x ) = x 1 + x 3 3 ! + x 2 n ? 1 ( 2 n ? 1 ) ! + . . . = e x ? e ? x 2 sin(x) = \frac{x}{1}+\frac{x^3}{3!}+\frac{x^{2n-1}}{(2n-1)!}+...=\frac{e^x - e^{-x}}{2} sin(x)=1x?+3!x3?+(2n?1)!x2n?1?+...=2ex?e?x?
c o s ( x ) = 1 + x 2 2 ! + x 4 4 ! + . . . + x 2 n 2 n ! + . . . = e ? x + e x 2 cos(x)=1+\frac{x^2}{2!}+\frac{x^4}{4!}+...+\frac{x^{2n}}{2n!}+...=\frac{e^{-x}+e^x}{2} cos(x)=1+2!x2?+4!x4?+...+2n!x2n?+...=2e?x+ex?


2m 1n 1r

組合 球相同 盒子不同 不能是空 C n ? 1 m ? 1 \quad C_{n-1}^{m-1} Cn?1m?1?







數(shù)的拆分


把正整數(shù) 拆分成 a b c 的和的方法P(n)
1 ( 1 ? x a ) ( 1 ? x b ) ( 1 ? x c ) = ( 1 + x a + x 2 a + . . . ) ( 1 + x b + x 2 b + . . . ) ( 1 + x c + x 2 c + . . . ) \frac{1}{(1-x^a)(1-x^b)(1-x^c)}=(1+x^a+x^{2a}+...)(1+x^b+x^{2b}+...)(1+x^c+x^{2c}+...) (1?xa)(1?xb)(1?xc)1?=(1+xa+x2a+...)(1+xb+x2b+...)(1+xc+x2c+...)

( 1 + x ) ( 1 + x 2 ) ( 1 + x 3 ) ( 1 + x 4 ) (1+x)(1+x^2)(1+x^3)(1+x^4) (1+x)(1+x2)(1+x3)(1+x4)

1 ? x 2 = 1 + x 1 ? x 1-x^2 = \frac {1+x}{1-x} 1?x2=1?x1+x?
1 + x 2 = 1 ? x 4 1 ? x 2 1+x^2 = \frac{1-x^4}{1-x^2} 1+x2=1?x21?x4?
1 ? x 2 n 1 ? x = 1 + x + x 2 + . . . + x 2 n ? 1 \frac{1-x^{2n}}{1-x}=1+x+x^2+...+x^{2n-1} 1?x1?x2n?=1+x+x2+...+x2n?1





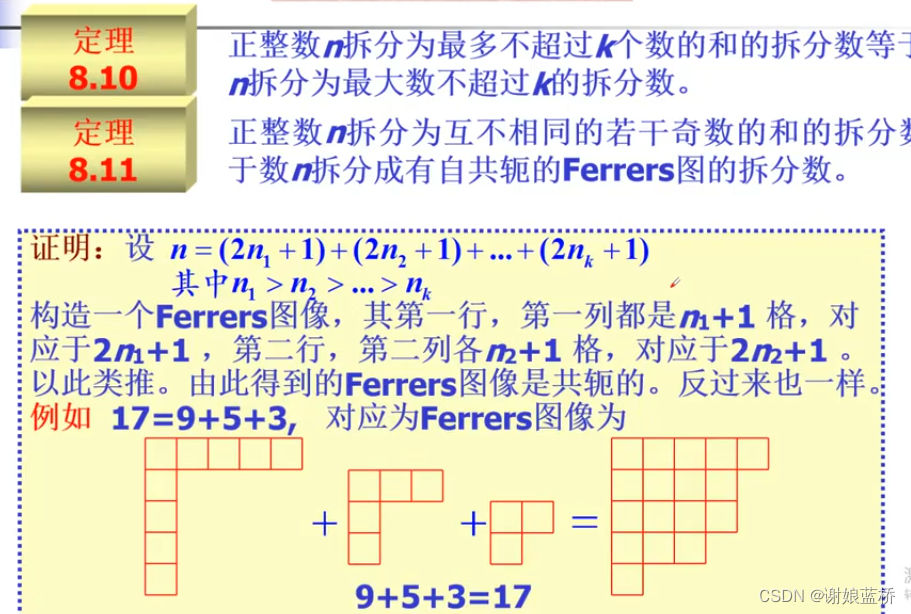
遞推關(guān)系

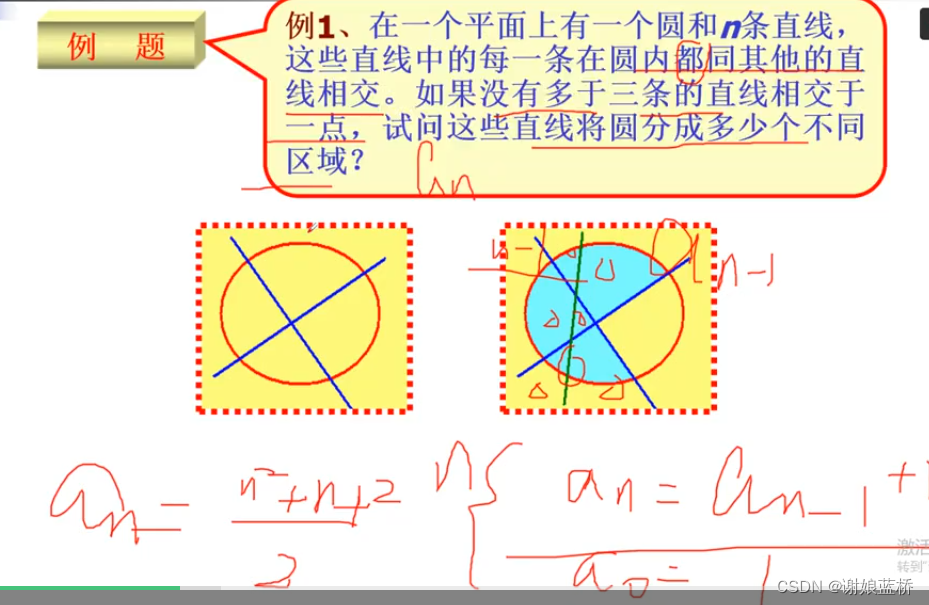


F n ? F n ? 1 ? F n ? 2 = 0 F n ? 1 ? F n ? 2 ? F n ? 3 = 0 F_n-F_{n-1}-F_{n-2}=0\\F_{n-1}-F_{n-2}-F_{n-3}=0 Fn??Fn?1??Fn?2?=0Fn?1??Fn?2??Fn?3?=0


C ( x ) = x n ? b 1 x n ? 1 ? b 2 x n ? 2 . . . = 0 C(x)=x^n-b_1x^{n-1}-b_2x^{n-2} ...=0 C(x)=xn?b1?xn?1?b2?xn?2...=0
常系數(shù)線性齊次遞推關(guān)系
1.遞推關(guān)系—
2.特征方程 線性齊次方程
3.求解-----特征根 q
由 a n = q n a_n=q^n an?=qn是方程的解 寫(xiě)出通解的形式,
將初值帶入即可得到遞推關(guān)系


{ a n = 2 a n ? 1 + a n ? 2 ? 2 a n ? 3 ( n ≥ 3 ) a 0 = 1 , a 1 = 2 ; a 2 = 0 \begin{cases} a_n=2a_{n-1}+a_n-2-2a_{n-3} \; (n\ge 3)\\ a_0=1,a_1=2;a_2=0\\ \end{cases} {an?=2an?1?+an??2?2an?3?(n≥3)a0?=1,a1?=2;a2?=0?
求遞推關(guān)系
x 3 ? 2 x 2 ? x + 2 = 0 x^3-2x^2-x+2=0 x3?2x2?x+2=0
(x+1)(x-1)(x-2)=0
特征根是 -1 1 2
q 1 = 1 q 2 = ? 1 q 3 = 2 q_1= 1 \quad q_2= -1 \quad q_3=2 q1?=1q2?=?1q3?=2
通解形式為 a n = c 1 q n + c 2 q n + c 3 q n a_n=c_1q^n+c_2q^n+c_3q^n an?=c1?qn+c2?qn+c3?qn 有幾個(gè)根有幾項(xiàng)

q 最終為1,忽略掉了


x 2 ? 2 x + 1 = 0 x^2-2x+1=0 x2?2x+1=0
特征根相同時(shí), q 1 = q 2 = 1 a n = c 1 + c 2 n q_1=q_2=1 \\ a_n= c_1 +c_2n q1?=q2?=1an?=c1?+c2?n

{ a n = ? a n ? 1 + 3 a n ? 2 + 5 a n ? 3 + 2 a n ? 4 ( n ≥ 4 ) a 0 = 1 , a 1 = 0 , a 2 = 1 , a 3 = 2 \begin{cases} a_n=-a_{n-1}+3a_n-2+5a_{n-3}+2a_{n-4} \; (n\ge 4)\\ a_0=1,a_1=0,a_2=1,a_3=2\\ \end{cases} {an?=?an?1?+3an??2+5an?3?+2an?4?(n≥4)a0?=1,a1?=0,a2?=1,a3?=2?
x 4 + x 3 ? 3 x 2 ? 5 x ? 2 = 0 q 1 = q 2 = q 3 = ? 1 , q 4 = 2 x^4+x^3-3x^2-5x-2=0\\ q1=q2=q3=-1 ,q4=2 x4+x3?3x2?5x?2=0q1=q2=q3=?1,q4=2多項(xiàng)式除法
a n = c 1 ( ? 1 ) n + c 2 n ( ? 1 ) n + c 3 n 2 ( ? 1 ) n + c 4 2 n a_n=c_1(-1)^n +c_2n(-1)^n+c_3n^2(-1)^n+c_42^n an?=c1?(?1)n+c2?n(?1)n+c3?n2(?1)n+c4?2n
{ a 0 = c 1 + c 4 = 1 a 1 = ? c 1 ? c 2 ? c 3 + 2 ? c 4 = 0 a 2 = c 1 + c 2 ? 2 + 4 c 3 + c 4 ? 4 = 1 a 3 = ? c 1 ? 3 c 2 ? 9 c 3 + 8 c 4 = 2 \begin{cases} a_0=c_1+c_4 = 1 \\ a_1=-c_1-c_2-c_3+2*c_4=0\\ a_2 = c_1 + c_2*2+4c_3+c_4*4=1\\ a_3 = -c_1 -3c_2-9c_3+8_c4=2 \end{cases} ? ? ??a0?=c1?+c4?=1a1?=?c1??c2??c3?+2?c4?=0a2?=c1?+c2??2+4c3?+c4??4=1a3?=?c1??3c2??9c3?+8c?4=2?
c 1 = 42 52 , c 2 = ? 29 52 , c 3 = 7 52 , c 4 = 10 52 c_1=\frac{42}{52},c_2=-\frac{29}{52},c_3=\frac{7}{52},c_4=\frac{10}{52} c1?=5242?,c2?=?5229?,c3?=527?,c4?=5210?
a n = 42 52 ( ? 1 ) n ? 29 52 n ( ? 1 ) n + 7 52 n 2 ( ? 1 ) n + 10 52 2 n a_n=\frac{42}{52}(-1)^n-\frac{29}{52}n(-1)^n+\frac{7}{52}n^2(-1)^n+\frac{10}{52}2^n an?=5242?(?1)n?5229?n(?1)n+527?n2(?1)n+5210?2n
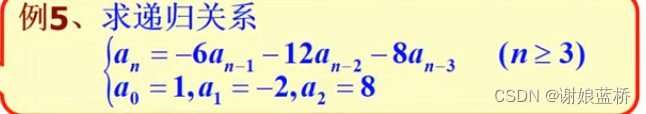
x 3 + 6 x 2 + 12 x + 8 = 0 ( x + 2 ) 3 = 0 x^3+6x^2+12x+8=0\\ (x+2)^3=0 x3+6x2+12x+8=0(x+2)3=0
( c 1 + c 2 n + c 3 n 2 = a n (c_1+c_2n+c_3n^2=a_n (c1?+c2?n+c3?n2=an?

常系數(shù)線性非齊次遞推關(guān)系
1.找出遞推關(guān)系
2.找出齊次遞推關(guān)系,求出齊次的通解,然后求特解,從而得到遞推關(guān)系
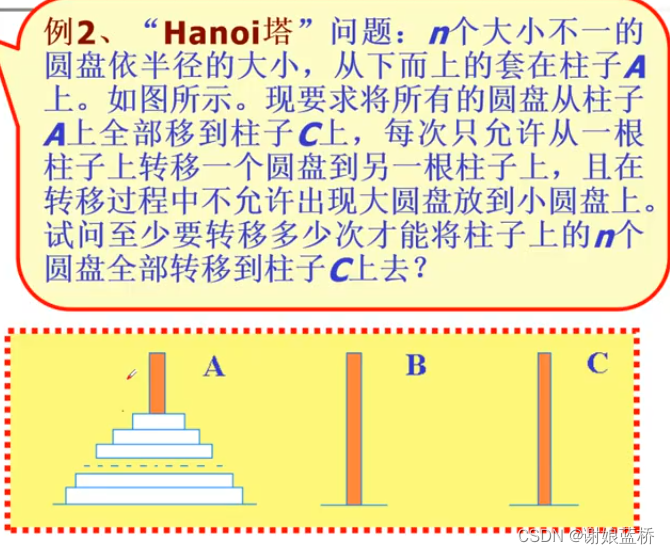
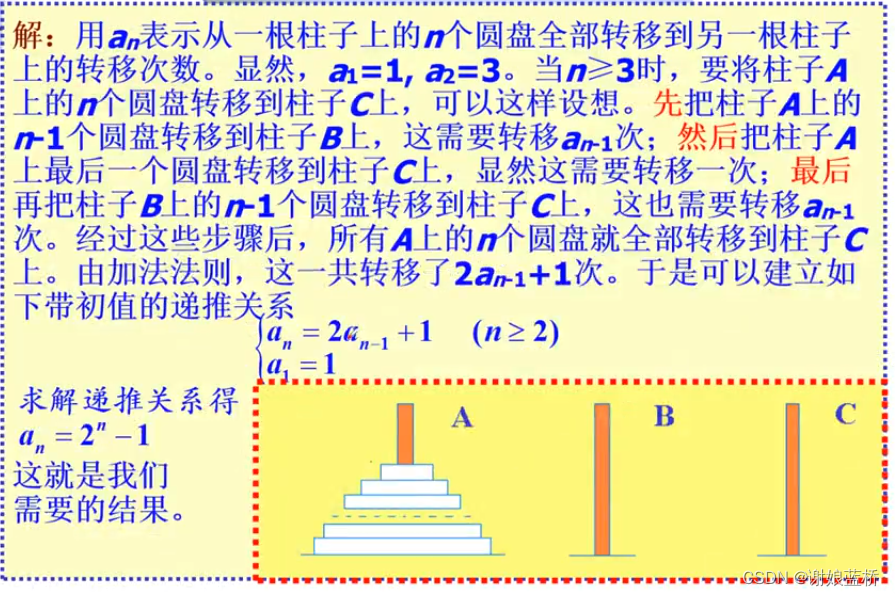
漢諾塔遞推關(guān)系

求解齊次方程 a n ? 2 a n ? 1 = 0 a_n-2a_{n-1}=0 an??2an?1?=0
特征方程 q =2
a n ? = c ? 2 n a_n^*=c *2^n an??=c?2n
由于f(n)=1 (上面丟掉的)

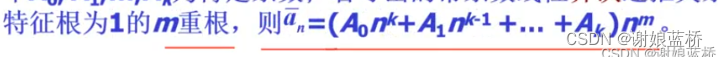
m=1 n=1 k=0 an=A
a2=3 = c1*2^n+A
A=-1