python做調(diào)查問(wèn)卷網(wǎng)站百度指數(shù)批量
背包問(wèn)題概述
背包問(wèn)題 (Knapsack problem) 是?種組合優(yōu)化的 NP完全問(wèn)題 。
問(wèn)題可以描述為:給定?組物品,每種物品都有??的重量和價(jià)格,在限定的總重量?jī)?nèi),我們?nèi)绾芜x擇,才能使得物品的總價(jià)格最?。
根據(jù)物品的個(gè)數(shù),分為如下?類:
? 01 背包問(wèn)題:每個(gè)物品只有?個(gè)
? 完全背包問(wèn)題:每個(gè)物品有?限多個(gè)
? 多重背包問(wèn)題:每件物品最多有 si 個(gè)
? 混合背包問(wèn)題:每個(gè)物品會(huì)有上?三種情況......
? 分組背包問(wèn)題:物品有 n 組,每組物品?有若?個(gè),每組?最多選?個(gè)物品
其中上述分類??,根據(jù)背包是否裝滿,?分為兩類:
? 不?定裝滿背包
? 背包?定裝滿
優(yōu)化?案:
? 空間優(yōu)化 - 滾動(dòng)數(shù)組
? 單調(diào)隊(duì)列優(yōu)化
? 貪?優(yōu)化
根據(jù)限定條件的個(gè)數(shù),?分為兩類:
? 限定條件只有?個(gè):?如體積 -> 普通的背包問(wèn)題
? 限定條件有兩個(gè):?如體積 + 重量 -> ?維費(fèi)?背包問(wèn)題
根據(jù)不同的問(wèn)法,?分為很多類:
? 輸出?案
? 求?案總數(shù)
? 最優(yōu)?案
? ?案可?性
其實(shí)還有很多分類,但是我們僅需了解即可。因此,背包問(wèn)題種類?常繁多,題型?常豐富,難度也是?常難以捉摸。但是,盡管種類?常多,都是從 01 背包問(wèn)題演化過(guò)來(lái)的。所以,?定要把 01 背包問(wèn)題學(xué)好。
01 背包問(wèn)題
例題一

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
背包問(wèn)題的狀態(tài)表??常經(jīng)典,如果?家不知道怎么來(lái)的,就把它當(dāng)成?個(gè)「模板」記住吧~
我們先解決第?問(wèn):
1. 狀態(tài)表?:
dp[i][j] 表?:從前 i 個(gè)物品中挑選,總體積「不超過(guò)」 j ,所有的選法中,能挑選出來(lái)的最?價(jià)值。
2. 狀態(tài)轉(zhuǎn)移?程:
線性 dp 狀態(tài)轉(zhuǎn)移?程分析?式,?般都是根據(jù)「最后?步」的狀況,來(lái)分情況討論:
i. 不選第 i 個(gè)物品:相當(dāng)于就是去前 i - 1 個(gè)物品中挑選,并且總體積不超過(guò) j 。此時(shí) dp[i][j] = dp[i - 1][j] ;
ii. 選擇第 i 個(gè)物品:那么我就只能去前 i - 1 個(gè)物品中,挑選總體積不超過(guò) j - v[i]的物品。此時(shí) dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是這種狀態(tài)不?定存在,因此需要特判?下。
綜上,狀態(tài)轉(zhuǎn)移?程為: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]) 。
3. 初始化:
我們多加??,?便我們的初始化,此時(shí)僅需將第??初始化為 0 即可。因?yàn)槭裁匆膊贿x,也能滿?體積不?于 j 的情況,此時(shí)的價(jià)值為 0 。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們僅需「從上往下」填表即可。
5. 返回值:
根據(jù)「狀態(tài)表?」,返回 dp[n][V] 。
接下來(lái)解決第?問(wèn):
第?問(wèn)僅需微調(diào)?下 dp 過(guò)程的五步即可。
因?yàn)橛锌赡軠惒? j 體積的物品,因此我們把不合法的狀態(tài)設(shè)置為 -1 。
1. 狀態(tài)表?:
dp[i][j] 表?:從前 i 個(gè)物品中挑選,總體積「正好」等于 j ,所有的選法中,能挑選出來(lái)的最?價(jià)值。
2. 狀態(tài)轉(zhuǎn)移?程:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]) 。 但是在使? dp[i - 1][j - v[i]] 的時(shí)候,不僅要判斷 j >= v[i] ,?要判斷 dp[i - 1][j - v[i]] 表?的情況是否存在,也就是 dp[i - 1][j - v[i]] != -1 。
3. 初始化:
我們多加??,?便我們的初始化:
i. 第?個(gè)格?為 0 ,因?yàn)檎媚軠?體積為 0 的背包;
ii. 但是第??后?的格?都是 -1 ,因?yàn)闆](méi)有物品,?法滿?體積?于 0 的情況。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們僅需「從上往下」填表即可。
5. 返回值:
由于最后可能湊不成體積為 V 的情況,因此返回之前需要「特判」?下。

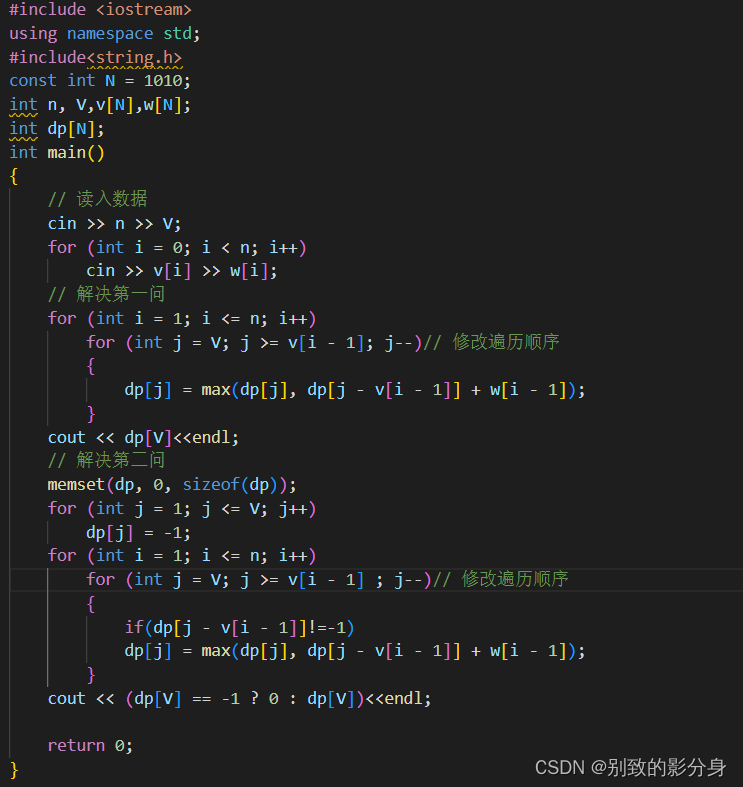
空間優(yōu)化:
背包問(wèn)題基本上都是利?「滾動(dòng)數(shù)組」來(lái)做空間上的優(yōu)化:
i. 利?「滾動(dòng)數(shù)組」優(yōu)化;
ii. 直接在「原始代碼」上修改。
在01背包問(wèn)題中,優(yōu)化的結(jié)果為:
i. 刪掉所有的橫坐標(biāo);
ii. 修改?下 j 的遍歷順序。
例題二

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
先將問(wèn)題轉(zhuǎn)化成我們「熟悉」的題型。如果數(shù)組能夠被分成兩個(gè)相同元素之和相同的?集,那么原數(shù)組必須有下??個(gè)性質(zhì):
i. 所有元素之和應(yīng)該是?個(gè)偶數(shù);
ii. 數(shù)組中最?的元素應(yīng)該?于所有元素總和的?半;
iii. 挑選?些數(shù),這些數(shù)的總和應(yīng)該等于數(shù)組總和的?半。
根據(jù)前兩個(gè)性質(zhì),我們可以提前判斷數(shù)組能夠被劃分。根據(jù)最后?個(gè)性質(zhì),我們發(fā)現(xiàn)問(wèn)題就轉(zhuǎn)化成
了「01 背包」的模型:
i. 數(shù)組中的元素只能選擇?次;
ii. 每個(gè)元素?臨被選擇或者不被選擇的處境;
iii. 選出來(lái)的元素總和要等于所有元素總和的?半。
其中,數(shù)組內(nèi)的元素就是物品,總和就是背包。那么我們就可以?背包模型的分析?式,來(lái)處理這道題。 請(qǐng)?家注意,「不要背」?fàn)顟B(tài)轉(zhuǎn)移?程,因?yàn)轭}型變化之后,狀態(tài)轉(zhuǎn)移?程就會(huì)跟著變化。我們要記住的是分析問(wèn)題的模式。?這種分析問(wèn)題的模式來(lái)解決問(wèn)題。
1. 狀態(tài)表?:
dp[i][j] 表?在前 i 個(gè)元素中選擇,所有的選法中,能否湊成總和為 j 這個(gè)數(shù)。
2. 狀態(tài)轉(zhuǎn)移?程:
?規(guī)矩,根據(jù)「最后?個(gè)位置」的元素,結(jié)合題?的要求,分情況討論:
i. 不選擇 nums[i] :那么我們是否能夠湊成總和為 j ,就要看在前 i - 1 個(gè)元素中選,能否湊成總和為 j 。根據(jù)狀態(tài)表?,此時(shí) dp[i][j] = dp[i - 1][j] ;
ii. 選擇 nums[i] :這種情況下是有前提條件的,此時(shí)的 nums[i] 應(yīng)該是?于等于 j 。
因?yàn)槿绻@個(gè)元素都?要湊成的總和?,選擇它就沒(méi)有意義呀。那么我們是否能夠湊成總和為 j ,就要看在前 i - 1 個(gè)元素中選,能否湊成總和為 j - nums[i] 。根據(jù)狀態(tài)表?,此時(shí) dp[i][j] = dp[i - 1][j - nums[i]] 。
綜上所述,兩種情況下只要有?種能夠湊成總和為 j ,那么這個(gè)狀態(tài)就是 true 。因此,狀態(tài)轉(zhuǎn)移?程為: dp[i][j] = dp[i - 1][j]
if(nums[i - 1] <= j) dp[i][j] = dp[i][j] || dp[i - 1][j - nums[i-1]]
3. 初始化:
由于需要?到上??的數(shù)據(jù),因此我們可以先把第??初始化。第??表?不選擇任何元素,要湊成?標(biāo)和 j 。只有當(dāng)?標(biāo)和為 0 的時(shí)候才能做到,因此第??僅需初始化第?個(gè)元素 dp[0][0] = true
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們需要「從上往下」填寫每??,每??的順序是「?所謂的」。
5. 返回值: ?
根據(jù)「狀態(tài)表?」,返回 dp[n][aim] 的值。其中 n 表?數(shù)組的??, aim 表?要湊的?標(biāo)和。

6. 空間優(yōu)化:
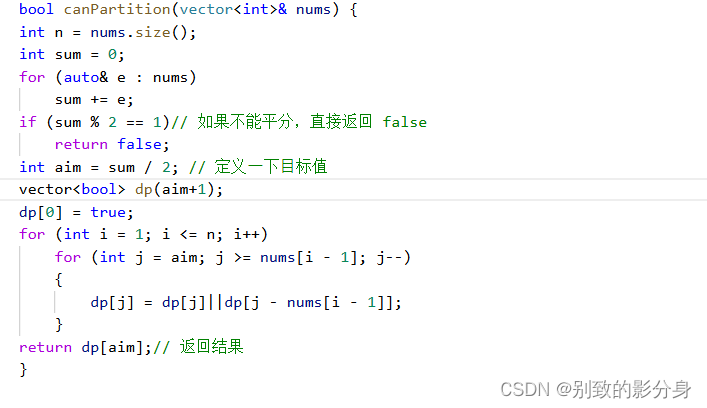
所有的「背包問(wèn)題」,都可以進(jìn)?空間上的優(yōu)化。
對(duì)于 01背包類型的,我們的優(yōu)化策略是:
i. 刪掉第?維;
ii. 修改第?層循環(huán)的遍歷順序即可。
例題三

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
本題可以直接?「暴搜」的?法解決。但是稍微?數(shù)學(xué)知識(shí)分析?下,就能轉(zhuǎn)化成我們常?的「背
包模型」的問(wèn)題。設(shè)我們最終選取的結(jié)果中,前?加 + 號(hào)的數(shù)字之和為 a ,前?加 - 號(hào)的數(shù)字之和為 b ,整個(gè)數(shù)組的總和為 sum ,于是我們有:
? a + b = sum
? a - b = target
上?兩個(gè)式?消去 b 之后,可以得到 a = (sum + target) / 2,也就是說(shuō),我們僅需在 nums 數(shù)組中選擇?些數(shù),將它們湊成和為 (sum + target) / 2 即可。問(wèn)題就變成了 416. 分割等和?集 這道題。
我們可以?相同的分析模式,來(lái)處理這道題。
1. 狀態(tài)表?:
dp[i][j] 表?:在前 i 個(gè)數(shù)中選,總和正好等于 j ,?共有多少種選法。
2. 狀態(tài)轉(zhuǎn)移?程:
?規(guī)矩,根據(jù)「最后?個(gè)位置」的元素,結(jié)合題?的要求,我們有「選擇」最后?個(gè)元素或者「不
選擇」最后?個(gè)元素兩種策略:
i. 不選 nums[i] :那么我們湊成總和 j 的總?案,就要看在前 i - 1 個(gè)元素中選,湊成總和為 j 的?案數(shù)。根據(jù)狀態(tài)表?,此時(shí) dp[i][j] = dp[i - 1][j] ;
ii. 選擇 nums[i] :這種情況下是有前提條件的,此時(shí)的 nums[i] 應(yīng)該是?于等于 j 。
因?yàn)槿绻@個(gè)元素都?要湊成的總和?,選擇它就沒(méi)有意義呀。那么我們能夠湊成總和為 j 的?案數(shù),就要看在前 i - 1 個(gè)元素中選,能否湊成總和為 j - nums[i] 。根據(jù)狀態(tài)表?,此時(shí) dp[i][j] = dp[i - 1][j - nums[i]]
綜上所述,兩種情況如果存在的話,應(yīng)該要累加在?起。因此,狀態(tài)轉(zhuǎn)移?程為:
dp[i][j] = dp[i - 1][j]
if(nums[i - 1] <= j) dp[i][j] = dp[i][j] += dp[i - 1][j - nums[i - 1]]
3. 初始化:
由于需要?到「上??」的數(shù)據(jù),因此我們可以先把第??初始化。第??表?不選擇任何元素,要湊成?標(biāo)和 j 。只有當(dāng)?標(biāo)和為 0 的時(shí)候才能做到,因此第??僅需初始化第?個(gè)元素 dp[0][0] = 1
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們需要「從上往下」填寫每??,每??的順序是「?所謂的」。
5. 返回值:
根據(jù)「狀態(tài)表?」,返回 dp[n][aim] 的值。其中 n 表?數(shù)組的??, aim 表?要湊的?標(biāo)和。

6. 空間優(yōu)化:
所有的「背包問(wèn)題」,都可以進(jìn)?空間上的優(yōu)化。
對(duì)于 01背包類型的,我們的優(yōu)化策略是:
i. 刪掉第?維;
ii. 修改第?層循環(huán)的遍歷順序即可。

例題四

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
先將問(wèn)題「轉(zhuǎn)化」成我們熟悉的題型。
? 任意兩塊?頭在?起粉碎,重量相同的部分會(huì)被丟掉,重量有差異的部分會(huì)被留下來(lái)。那就相當(dāng)于在原始的數(shù)據(jù)的前?,加上「加號(hào)」或者「減號(hào)」,是最終的結(jié)果最?即可。也就是說(shuō)把原始的?頭分成兩部分,兩部分的和越接近越好。
? ?因?yàn)楫?dāng)所有元素的和固定時(shí),分成的兩部分越接近數(shù)組「總和的?半」,兩者的差越?。
因此問(wèn)題就變成了:在數(shù)組中選擇?些數(shù),讓這些數(shù)的和盡量接近 sum / 2 ,如果把數(shù)看成物品,每個(gè)數(shù)的值看成體積和價(jià)值,問(wèn)題就變成了「01 背包問(wèn)題」。
1. 狀態(tài)表?:
dp[i][j] 表?在前 i 個(gè)元素中選擇,總和不超過(guò) j,此時(shí)所有元素的「最?和」。
2. 狀態(tài)轉(zhuǎn)移?程:
?規(guī)矩,根據(jù)「最后?個(gè)位置」的元素,結(jié)合題?的要求,分情況討論:
i. 不選 stones[i] :那么我們是否能夠湊成總和為 j ,就要看在前 i - 1 個(gè)元素中選,能否湊成總和為 j 。根據(jù)狀態(tài)表?,此時(shí) dp[i][j] = dp[i - 1][j] ;
ii. 選擇 stones[i] :這種情況下是有前提條件的,此時(shí)的 stones[i] 應(yīng)該是?于等于 j 。因?yàn)槿绻@個(gè)元素都?要湊成的總和?,選擇它就沒(méi)有意義呀。那么我們是否能夠湊成總和為 j ,就要看在前 i - 1 個(gè)元素中選,能否湊成總和為 j - stones[i] 。根據(jù)狀態(tài)表?,此時(shí) dp[i][j] = dp[i - 1][j -stones[i]] + stones[i] 。
綜上所述,我們要的是最?價(jià)值。因此,狀態(tài)轉(zhuǎn)移?程為:
dp[i][j] = dp[i - 1][j]
if(j >= stones[i]) dp[i][j] = max(dp[i][j] ,?dp[i - 1][j - stones[i]] + stones[i]) 。
3. 初始化:
由于需要?到上??的數(shù)據(jù),因此我們可以先把第??初始化。第??表?「沒(méi)有??」。因此想湊成?標(biāo)和 j ,最?和都是 0 。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們需要「從上往下」填寫每??,每??的順序是「?所謂的」。
5. 返回值:
a. 根據(jù)「狀態(tài)表?」,先找到最接近 sum / 2 的最?和 dp[n][sum / 2] ;
b. 因?yàn)槲覀円氖莾啥??的差,因此返回 sum - 2 * dp[n][sum / 2] 。

6. 空間優(yōu)化:
所有的背包問(wèn)題,都可以進(jìn)?「空間」上的優(yōu)化。
對(duì)于 01背包類型的,我們的優(yōu)化策略是:
i. 刪掉第?維;
ii. 修改第?層循環(huán)的「遍歷順序」即可。

完全背包問(wèn)題
例題一

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
背包問(wèn)題的狀態(tài)表??常經(jīng)典,如果?家不知道怎么來(lái)的,就把它當(dāng)成?個(gè)模板記住吧~
我們先解決第?問(wèn):
1. 狀態(tài)表?:
dp[i][j] 表?:從前 i 個(gè)物品中挑選,總體積不超過(guò) j ,所有的選法中,能挑選出來(lái)的最?價(jià)值.(這?是和 01背包?樣噠)
2. 狀態(tài)轉(zhuǎn)移?程:
線性 dp 狀態(tài)轉(zhuǎn)移?程分析?式,?般都是根據(jù)最后?步的狀況,來(lái)分情況討論。但是最后?個(gè)物品能選很多個(gè),因此我們的需要分很多情況:
i. 選 0 個(gè)第 i 個(gè)物品:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)物品中挑選,總體積不超過(guò) j 。此時(shí)最?價(jià)值為 dp[i - 1][j] ;
ii. 選 1 個(gè)第 i 個(gè)物品:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)物品中挑選,總體積不超過(guò) j - v[i] 。因?yàn)樘暨x了?個(gè) i 物品,此時(shí)最?價(jià)值為 dp[i - 1][j - v[i]] + w[i] ;
iii. 選 2 個(gè)第 i 個(gè)物品:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)物品中挑選,總體積不超過(guò) j - 2 * v[i] 。因?yàn)樘暨x了兩個(gè) i 物品,此時(shí)最?價(jià)值為 dp[i - 1][j - 2 * v[i]] + 2 * w[i] ;
iv. ......
綜上,我們的狀態(tài)轉(zhuǎn)移?程為:
dp[i][j]=max(dp[i-1][j], dp[i-1][j-v[i]]+w[i], dp[i-1][j- 2*v[i]]+2*w[i]...)
當(dāng)我們發(fā)現(xiàn),計(jì)算?個(gè)狀態(tài)的時(shí)候,需要?個(gè)循環(huán)才能搞定的時(shí)候,我們要想到去優(yōu)化。優(yōu)化的?
向就是??個(gè)或者兩個(gè)狀態(tài)來(lái)表?這?堆的狀態(tài),通常就是?數(shù)學(xué)的?式做?下等價(jià)替換。我們發(fā)
現(xiàn)第?維是有規(guī)律的變化的,因此我們?nèi)タ纯? dp[i][j - v[i]] 這個(gè)狀態(tài):
dp[i][j-v[i]]=max(dp[i-1][j-v[i]],dp[i-1][j-2*v[i]]+w[i],dp[i-1] [j-3*v[i]]+2*w[i]...)
我們發(fā)現(xiàn),把 dp[i][j - v[i]] 加上 w[i] 正好和 dp[i][j] 中除了第?項(xiàng)以外的全部?致,因此我們可以修改我們的狀態(tài)轉(zhuǎn)移?程為: dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]) 。
3. 初始化:
我們多加??,?便我們的初始化,此時(shí)僅需將第??初始化為 0 即可。因?yàn)槭裁匆膊贿x,也能 滿?體積不?于 j 的情況,此時(shí)的價(jià)值為 0 。
4. 填表順序:
根據(jù)狀態(tài)轉(zhuǎn)移?程,我們僅需從上往下填表即可。
5. 返回值:
根據(jù)狀態(tài)表?,返回 dp[n][V] 。
接下來(lái)解決第?問(wèn):
第?問(wèn)僅需微調(diào)?下 dp 過(guò)程的五步即可。因?yàn)橛锌赡軠惒? j 體積的物品,因此我們把不合法的狀態(tài)設(shè)置為 -1 。
1. 狀態(tài)表?:
dp[i][j] 表?:從前 i 個(gè)物品中挑選,總體積正好等于 j ,所有的選法中,能挑選出來(lái)的最?價(jià)值。
2. 狀態(tài)轉(zhuǎn)移?程:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]) 。
但是在使? dp[i][j - v[i]] 的時(shí)候,不僅要判斷 j >= v[i] ,?要判斷 dp[i][j - v[i]] 表?的情況是否存在,也就是 dp[i][j - v[i]] != -1 。
3. 初始化:
我們多加??,?便我們的初始化:
i. 第?個(gè)格?為 0 ,因?yàn)檎媚軠?體積為 0 的背包;
ii. 但是第??后?的格?都是 -1 ,因?yàn)闆](méi)有物品,?法滿?體積?于 0 的情況。
4. 填表順序:
根據(jù)狀態(tài)轉(zhuǎn)移?程,我們僅需從上往下填表即可。
5. 返回值:
由于最后可能湊不成體積為 V 的情況,因此返回之前需要特判?下。

空間優(yōu)化:
背包問(wèn)題基本上都是利?滾動(dòng)數(shù)組來(lái)做空間上的優(yōu)化:
i. 利?滾動(dòng)數(shù)組優(yōu)化;
ii. 直接在原始代碼上修改。
在完全背包問(wèn)題中,優(yōu)化的結(jié)果為:
i. 僅需刪掉所有的橫坐標(biāo)。

例題二
解法(動(dòng)態(tài)規(guī)劃):
算法思路:
先將問(wèn)題「轉(zhuǎn)化」成我們熟悉的題型。
i. 在?些物品中「挑選」?些出來(lái),然后在滿?某個(gè)「限定條件」下,解決?些問(wèn)題,?概率是「背包」模型;
ii. 由于每?個(gè)物品都是?限多個(gè)的,因此是?個(gè)「完全背包」問(wèn)題。
接下來(lái)的分析就是基于「完全背包」的?式來(lái)的。
1. 狀態(tài)表?:
dp[i][j] 表?:從前 i 個(gè)硬幣中挑選,總和正好等于 j ,所有的選法中,最少的硬幣個(gè)數(shù)。
2. 狀態(tài)轉(zhuǎn)移?程:
線性 dp 狀態(tài)轉(zhuǎn)移?程分析?式,?般都是根據(jù)「最后?步」的狀況,來(lái)分情況討論。但是最后?個(gè)物品能選很多個(gè),因此我們的需要分很多情況:
i. 選 0 個(gè)第 i 個(gè)硬幣:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)硬幣中挑選,總和正好等于 j 。此時(shí)最少的硬幣個(gè)數(shù)為 dp[i - 1][j] ;
ii. 選 1 個(gè)第 i 個(gè)硬幣:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)硬幣中挑選,總和正好等于 j - v[i] 。因?yàn)樘暨x了?個(gè) i 硬幣,此時(shí)最少的硬幣個(gè)數(shù)為 dp[i - 1][j - coins[i]] + 1 ;
iii. 選 2 個(gè)第 i 個(gè)硬幣:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)硬幣中挑選,總和正好等于 j - 2 * coins 。因?yàn)樘暨x了兩個(gè) i 硬幣,此時(shí)最少的硬幣個(gè)數(shù)為 dp[i - 1][j - 2 * coins[i]] + 2 ;
iv. ......
結(jié)合我們?cè)谕耆嘲??的優(yōu)化思路,我們最終得到的狀態(tài)轉(zhuǎn)移?程為:
dp[i][j] = min(dp[i - 1][j], dp[i][j - coins[i]] + 1) 。
這?教給?家?個(gè)技巧,就是相當(dāng)于把第?種情況 dp[i - 1][j - coins[i]] + 1 ??的 i - 1 變成 i 即可。
3. 初始化:
初始化第??即可。這?因?yàn)槿?min ,所以我們可以把?效的地?設(shè)置成?窮? (0x3f3f3f3f)
因?yàn)檫@?要求正好湊成總和為 j ,因此,需要把第??除了第?個(gè)位置的元素,都設(shè)置成?窮?。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們僅需「從上往下」填表即可。
5. 返回值:
根據(jù)「狀態(tài)表?」,返回 dp[n][V] 。但是要特判?下,因?yàn)橛锌赡軠惒坏健?/span>

空間優(yōu)化后的算法代碼:
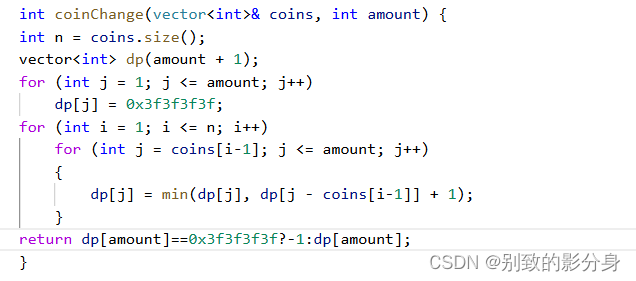
例題三

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
先將問(wèn)題「轉(zhuǎn)化」成我們熟悉的題型。
i. 在?些物品中「挑選」?些出來(lái),然后在滿?某個(gè)「限定條件」下,解決?些問(wèn)題,?概率是背包模型;
ii. 由于每?個(gè)物品都是?限多個(gè)的,因此是?個(gè)「完全背包」問(wèn)題。接下來(lái)的分析就是基于「完全背包」的?式來(lái)的。
1. 狀態(tài)表?:
dp[i][j] 表?:從前 i 個(gè)硬幣中挑選,總和正好等于 j ,?共有多少種選法。
2. 狀態(tài)轉(zhuǎn)移?程:
線性 dp 狀態(tài)轉(zhuǎn)移?程分析?式,?般都是「根據(jù)最后?步」的狀況,來(lái)分情況討論。但是最后?個(gè)物品能選很多個(gè),因此我們的需要分很多情況:
i. 選 0 個(gè)第 i 個(gè)硬幣:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)硬幣中挑選,總和正好等于 j 。此時(shí)選法個(gè)數(shù)為 dp[i - 1][j] ;
ii. 選 1 個(gè)第 i 個(gè)硬幣:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)硬幣中挑選,總和正好等于 j - v[i] 。因?yàn)樘暨x了?個(gè) i 硬幣,此時(shí)選法個(gè)數(shù)為 dp[i - 1][j - coins[i]] ;
iii. 選 2 個(gè)第 i 個(gè)硬幣:此時(shí)相當(dāng)于就是去前 i - 1 個(gè)硬幣中挑選,總和正好等于 j - 2 * coins 。因?yàn)樘暨x了兩個(gè) i 硬幣,此時(shí)選法個(gè)數(shù)為 dp[i - 1][j - 2 * coins[i]] ;
iv. ......
結(jié)合我們?cè)谕耆嘲??的「優(yōu)化思路」,我們最終得到的狀態(tài)轉(zhuǎn)移?程為:
dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]] 。
3. 初始化:
初始化第??即可。
第??表?沒(méi)有物品,沒(méi)有物品正好能湊能和為 0 的情況。因此 dp[0][0] = 1 ,其余位置都是 0 種情況。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們僅需「從上往下」填表即可。
5. 返回值:
根據(jù)「狀態(tài)表?」,返回 dp[n][V] 。

空間優(yōu)化后的算法代碼:

例題四

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
這?給出?個(gè)?「拆分出相同?問(wèn)題」的?式,定義?個(gè)狀態(tài)表?。(?「完全背包」?式的解法
就仿照之前的分析模式就好啦~~)為了敘述?便,把和為 n 的完全平?數(shù)的最少數(shù)量簡(jiǎn)稱為「最?數(shù)量」。對(duì)于 12 這個(gè)數(shù),我們分析?下如何求它的最?數(shù)量。
? 如果 12 本?就是完全平?數(shù),我們不?算了,直接返回 1 ;
? 但是 12 不是完全平?數(shù),我們?cè)囍褑?wèn)題分解?下:
1. 情況?:拆出來(lái)?個(gè) 1 ,然后看看 11 的最?數(shù)量,記為 x1 ;
2. 情況?:拆出來(lái)?個(gè) 4 ,然后看看 8 的最?數(shù)量,記為 x2 ;(為什么拆出來(lái) 4 ,?不拆出來(lái) 2 呢?)
3. 情況三:拆出來(lái)?個(gè) 8 ......
其中,我們接下來(lái)求 11 、 8 的時(shí)候,其實(shí)?回到了原來(lái)的問(wèn)題上。因此,我們可以嘗試? dp 的策略,將 1 2 3 4 6 等等這些數(shù)的最?數(shù)量依次保存起來(lái)。再求較?的 n 的時(shí)候,直接查表,然后找出最?數(shù)量。
1. 狀態(tài)表?:
dp[i] 表?:和為 i 的完全平?數(shù)的最少數(shù)量。
2. 狀態(tài)轉(zhuǎn)移?程:
對(duì)于 dp[i] ,根據(jù)思路那?的分析我們知道,可以根據(jù)?于等于 i 的所有完全平?數(shù) x 進(jìn)?劃分:
? x = 1 時(shí),最?數(shù)量為: 1 + dp[i - 1] ;
? x = 4 時(shí),最?數(shù)量為: 1 + dp[i - 4] ......
?直枚舉到 x <= i 為?。
為了?便枚舉完全平?數(shù),我們采?下?的策略: for(int j = 1; j * j <= i; j++)
綜上所述,狀態(tài)轉(zhuǎn)移?程為: dp[i] = min(dp[i], dp[i - j * j] + 1)
3. 初始化:
當(dāng) n = 0 的時(shí)候,沒(méi)法拆分,結(jié)果為 0 ; 當(dāng) n = 1 的時(shí)候,顯然為 1 。
4. 填表順序:
從左往右。
5. 返回值:
根據(jù)題意,返回 dp[n] 的值。

空間優(yōu)化后的算法代碼:

?維費(fèi)?的背包問(wèn)題
例題一

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
先將問(wèn)題轉(zhuǎn)化成我們熟悉的題型。
i. 在?些物品中「挑選」?些出來(lái),然后在滿?某個(gè)「限定條件」下,解決?些問(wèn)題,?概率是背包模型;
ii. 由于每?個(gè)物品都只有 1 個(gè),因此是?個(gè)「01 背包問(wèn)題」。
但是,我們發(fā)現(xiàn)這?道題??有「兩個(gè)限制條件」。因此是?個(gè)「?維費(fèi)?的 01 背包問(wèn)題」。那
么我們定義狀態(tài)表?的時(shí)候,來(lái)?個(gè)三維 dp 表,把第?個(gè)限制條件加上即可。
1. 狀態(tài)表?:
dp[i][j][k] 表?:從前 i 個(gè)字符串中挑選,字符 0 的個(gè)數(shù)不超過(guò) j ,字符 1 的個(gè)數(shù)不超過(guò) k ,所有的選法中,最?的?度。
2. 狀態(tài)轉(zhuǎn)移?程:
線性 dp 狀態(tài)轉(zhuǎn)移?程分析?式,?般都是「根據(jù)最后?步」的狀況,來(lái)分情況討論。為了?便敘述,我們記第 i 個(gè)字符中,字符 0 的個(gè)數(shù)為 a ,字符 1 的個(gè)數(shù)為 b :
i. 不選第 i 個(gè)字符串:相當(dāng)于就是去前 i - 1 個(gè)字符串中挑選,并且字符 0 的個(gè)數(shù)不超過(guò) j ,字符 1 的個(gè)數(shù)不超過(guò) k 。此時(shí)的最??度為 dp[i][j][k] = dp[i - 1] [j][k] ;
ii. 選擇第 i 個(gè)字符串:那么接下來(lái)我僅需在前 i - 1 個(gè)字符串??,挑選出來(lái)字符 0 的個(gè)數(shù)不超過(guò) j - a ,字符 1 的個(gè)數(shù)不超過(guò) k - b 的最??度,然后在這個(gè)?度后?加上字符串 i 即可。此時(shí) dp[i][j][k] = dp[i - 1][j - a][k - b] + 1 。 但是這種狀態(tài)不?定存在,因此需要特判?下。
綜上,狀態(tài)轉(zhuǎn)移?程為: dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j - a] [k - b] + 1) 。
3. 初始化:
當(dāng)沒(méi)有字符串的時(shí)候,沒(méi)有?度,因此初始化為 0 即可。
4. 填表順序:
保證第?維的循環(huán)「從?到?」即可。
5. 返回值:
根據(jù)「狀態(tài)表?」,我們返回 dp[len][m][n] 。 其中 len 表?字符串?dāng)?shù)組的?度。

6. 空間優(yōu)化:
所有的「背包問(wèn)題」,都可以進(jìn)?空間上的優(yōu)化。
對(duì)于「?維費(fèi)?的 01 背包」類型的,我們的優(yōu)化策略是:
i. 刪掉第?維;
ii. 修改第?層以及第三層循環(huán)的遍歷順序即可。

例題二

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
這道題??常難讀懂,但是如果結(jié)合例?多讀?遍,你就會(huì)發(fā)現(xiàn)是?個(gè)經(jīng)典的「?維費(fèi)?的背包問(wèn) 題」。因此我們可以仿照「?維費(fèi)?的背包」來(lái)定義狀態(tài)表?。
1. 狀態(tài)表?:
dp[i][j][k] 表?:從前 i 個(gè)計(jì)劃中挑選,總?數(shù)不超過(guò) j ,總利潤(rùn)?少為 k ,?共有多少種選法。
注意注意注意,這道題??出現(xiàn)了?個(gè)「?少」,和我們之前做過(guò)的背包問(wèn)題不?樣。因此,我們 在分析「狀態(tài)轉(zhuǎn)移?程」的時(shí)候要結(jié)合實(shí)際情況考慮?下。
2. 狀態(tài)轉(zhuǎn)移?程:
?規(guī)矩,根據(jù)「最后?個(gè)位置」的元素,結(jié)合題?的要求,我們有「選擇」最后?個(gè)元素或者「不
選擇」最后?個(gè)元素兩種策略:
i. 不選 i 位置的計(jì)劃:那我們只能去前 i - 1 個(gè)計(jì)劃中挑選,總?數(shù)不超過(guò) j ,總利潤(rùn)?少為 k 。此時(shí)?共有 dp[i - 1][j][k] 種選法;
ii. 選擇 i 位置的計(jì)劃:那我們?cè)谇? i - 1 個(gè)計(jì)劃中挑選的時(shí)候,限制就變成了,總?數(shù)不超過(guò) j - g[i] ,總利潤(rùn)?少為 k - p[i] 。此時(shí)?共有 dp[i - 1][j - g[i]][k - p[i]] 。
第?種情況下有兩個(gè)細(xì)節(jié)需要注意:
1. j - g[i] < 0 :此時(shí)說(shuō)明 g[i] 過(guò)?,也就是?數(shù)過(guò)多。因?yàn)槲覀兊臓顟B(tài)表?要求?數(shù)是不能超過(guò) j 的,因此這個(gè)狀態(tài)是不合法的,需要舍去。
2. k - p[i] < 0 :此時(shí)說(shuō)明 p[i] 過(guò)?,也就是利潤(rùn)太?。但是利潤(rùn)?,不正是我們想要的嘛?所以這個(gè)狀態(tài)「不能舍去」。但是問(wèn)題來(lái)了,我們的 dp 表是沒(méi)有負(fù)數(shù)的下標(biāo)的,這就意味著這些狀態(tài)我們?法表?。其實(shí),根本不需要負(fù)的下標(biāo),我們根據(jù)實(shí)際情況來(lái)看,如果這個(gè)任務(wù)的利潤(rùn)已經(jīng)能夠達(dá)標(biāo)了,我們僅需在之前的任務(wù)中,挑選出來(lái)的利潤(rùn)?少為 0 就可以了。因?yàn)閷?shí)際情況不允許我們是負(fù)利潤(rùn),那么負(fù)利潤(rùn)就等價(jià)于利潤(rùn)?少為 0 的情況。所以說(shuō)這種情況就等價(jià)于 dp[i][j][0] ,我們可以對(duì) k - p[i] 的結(jié)果與 0 取?個(gè) max 。
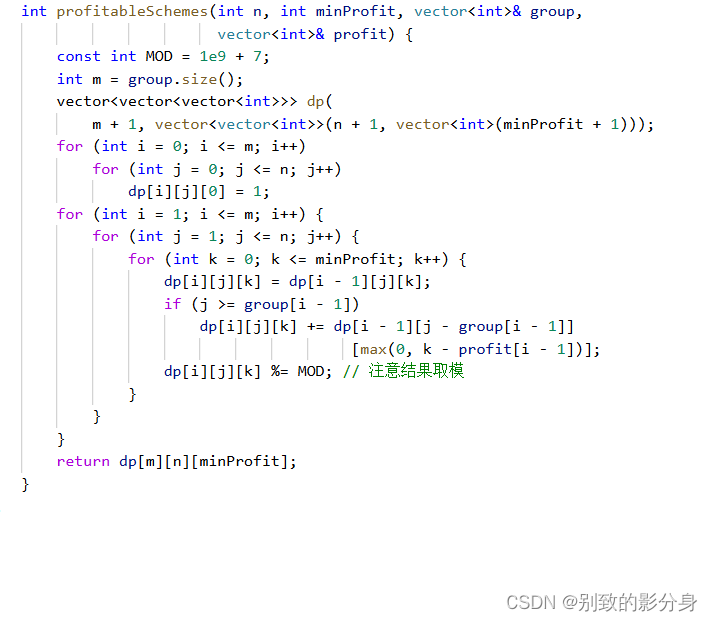
綜上,我們的狀態(tài)轉(zhuǎn)移?程為: dp[i][j][k] = dp[i - 1][j][k] + dp[i - 1][j - g[i - 1]][max(0, k - p[i - 1])] 。
3. 初始化:
當(dāng)我們的利潤(rùn)為 0 的時(shí)候,我們的利潤(rùn)為 0 ,此時(shí)?論?數(shù)限制為多少,我們都能找到?個(gè)「空集」的 ?案。因此初始化 dp[i][j][0] 的位置為 1 ,其中0 <= i?<= m,0 <= j <= n 。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,我們保證 i 從?到?即可。
5. 返回值:
根據(jù)「狀態(tài)表?」,我們返回 dp[len][m][n] 。
其中 len 表?字符串?dāng)?shù)組的?度。
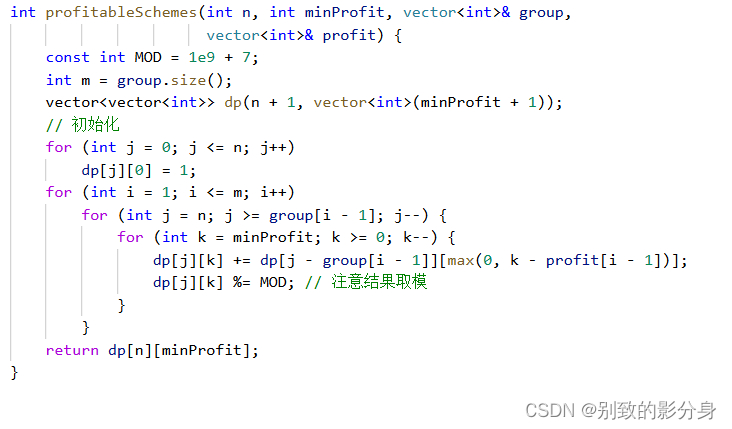
6. 空間優(yōu)化:
所有的「背包問(wèn)題」,都可以進(jìn)?空間上的優(yōu)化。
對(duì)于「?維費(fèi)?的 01 背包」類型的,我們的優(yōu)化策略是:
i. 刪掉第?維;
ii. 修改第?層以及第三層循環(huán)的遍歷順序即可。
似包?包
例題一

解法(動(dòng)態(tài)規(guī)劃):
算法思路:
?定要注意,我們的背包問(wèn)題本質(zhì)上求的是「組合」數(shù)問(wèn)題,?這?道題求的是「排列數(shù)」問(wèn)題。 因此我們不能被這道題給迷惑,還是?常規(guī)的 dp 思想來(lái)解決這道題。
1. 狀態(tài)表?:
這道題的狀態(tài)表?就是根據(jù)「拆分出相同?問(wèn)題」的?式,抽象出來(lái)?個(gè)狀態(tài)表?:當(dāng)我們?cè)谇?target 這個(gè)數(shù)?共有?種排列?式的時(shí)候,對(duì)于最后?個(gè)位置,如果我們拿出數(shù)組中的?個(gè)數(shù) x ,接下來(lái)就是去找 target - x ?共有多少種排列?式。因此我們可以抽象出來(lái)?個(gè)狀態(tài)表?:
dp[i] 表?:總和為 i 的時(shí)候,?共有多少種排列?案。
2. 狀態(tài)轉(zhuǎn)移?程:
對(duì)于 dp[i] ,我們根據(jù)「最后?個(gè)位置」劃分,我們可以選擇數(shù)組中的任意?個(gè)數(shù)nums[j] ,其中 0 <= j <= n - 1 。 當(dāng) nums[j] <= target 的時(shí)候,此時(shí)的排列數(shù)等于我們先找到 target - nums[j] 的?
案數(shù),然后在每?個(gè)?案后?加上?個(gè)數(shù)字 nums[j] 即可。因?yàn)橛泻芏鄠€(gè) j 符合情況,因此我們的狀態(tài)轉(zhuǎn)移?程為: dp[i] += dp[target - nums[j] ,其中 0 <= j <= n - 1 。
3. 初始化:
當(dāng)和為 0 的時(shí)候,我們可以什么都不選,「空集」?種?案,因此 dp[0] = 1 。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」易得「從左往右」。
5. 返回值:
根據(jù)「狀態(tài)表?」,我們要返回的是 dp[target] 的值。

卡特蘭數(shù)
例題一
解法(動(dòng)態(tài)規(guī)劃):
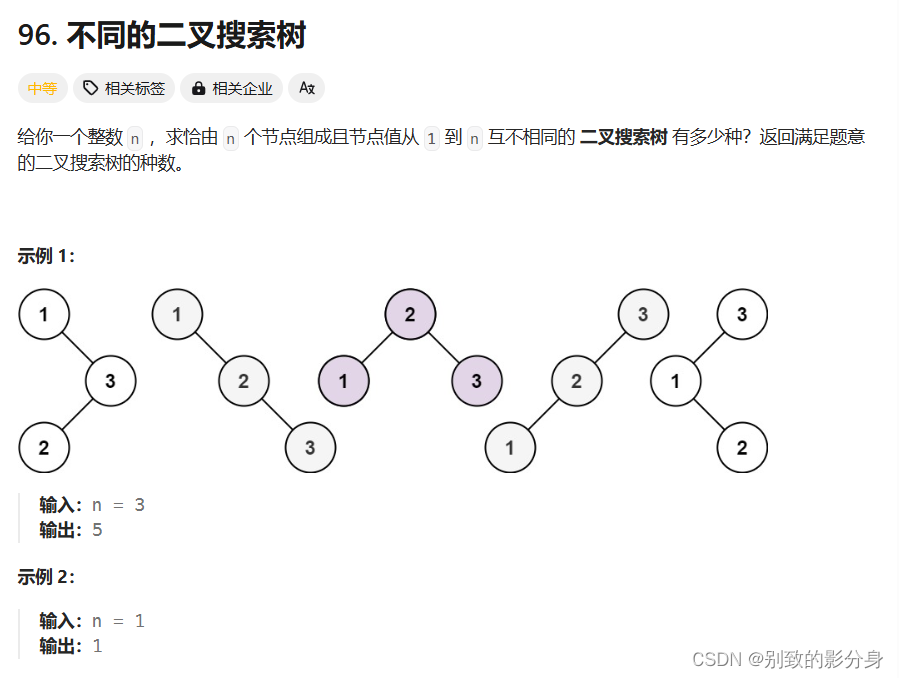
算法思路:
這道題屬于「卡特蘭數(shù)」的?個(gè)應(yīng)?,同樣能解決的問(wèn)題還有「合法的進(jìn)出棧序列」、「括號(hào)匹配
的括號(hào)序列」、「電影購(gòu)票」等等。如果感興趣的同學(xué)可以「百度」搜索卡特蘭數(shù),會(huì)有很多詳細(xì)
的介紹。
1. 狀態(tài)表?:
這道題的狀態(tài)表?就是根據(jù)「拆分出相同?問(wèn)題」的?式,抽象出來(lái)?個(gè)狀態(tài)表?:
當(dāng)我們?cè)谇髠€(gè)數(shù)為 n 的 BST 的個(gè)數(shù)的時(shí)候,當(dāng)確定?個(gè)根節(jié)點(diǎn)之后,左右?樹的結(jié)點(diǎn)「?jìng)€(gè)數(shù)」也確定了。此時(shí)左右?樹就會(huì)變成相同的?問(wèn)題,因此我們可以這樣定義狀態(tài)表?:dp[i] 表?:當(dāng)結(jié)點(diǎn)的數(shù)量為 i 個(gè)的時(shí)候,?共有多少顆 BST 。難的是如何推導(dǎo)狀態(tài)轉(zhuǎn)移?程,因?yàn)樗覀冎俺?的狀態(tài)轉(zhuǎn)移?程不是很像。
2. 狀態(tài)轉(zhuǎn)移?程:
對(duì)于 dp[i] ,此時(shí)我們已經(jīng)有 i 個(gè)結(jié)點(diǎn)了,為了?便敘述,我們將這 i 個(gè)結(jié)點(diǎn)排好序,并且編上 1, 2, 3, 4, 5.....i 的編號(hào)。那么,對(duì)于所有不同的 BST ,我們可以按照下?的劃分規(guī)則,分成不同的 i 類:「按照不同的頭結(jié)點(diǎn)來(lái)分類」。分類結(jié)果就是:
i. 頭結(jié)點(diǎn)為 1 號(hào)結(jié)點(diǎn)的所有 BST
ii. 頭結(jié)點(diǎn)為 2 號(hào)結(jié)點(diǎn)的所有 BST
iii. ......
如果我們能求出「每?類中的 BST 的數(shù)量」,將所有類的 BST 數(shù)量累加在?起,就是最后結(jié)果。 接下來(lái)選擇「頭結(jié)點(diǎn)為 j 號(hào)」的結(jié)點(diǎn),來(lái)分析這 i 類 BST 的通?求法。如果選擇「 j 號(hào)結(jié)點(diǎn)來(lái)作為頭結(jié)點(diǎn)」,根據(jù) BST 的定義:
i. j 號(hào)結(jié)點(diǎn)的「左?樹」的結(jié)點(diǎn)編號(hào)應(yīng)該在 [1, j - 1] 之間,?共有 j - 1 個(gè)結(jié)點(diǎn)。那么 j 號(hào)結(jié)點(diǎn)作為頭結(jié)點(diǎn)的話,它的「左?樹的種類」就有 dp[j - 1] 種(回顧?下我們 dp 數(shù)組的定義哈);
ii. j 號(hào)結(jié)點(diǎn)的「右?樹」的結(jié)點(diǎn)編號(hào)應(yīng)該在 [j + 1, i] 之間,?共有 i - j 個(gè)結(jié)點(diǎn)。那么 j 號(hào)結(jié)點(diǎn)作為頭結(jié)點(diǎn)的話,它的「右?樹的種類」就有 dp[i - j] 種;根據(jù)「排列組合」的原理可得: j 號(hào)結(jié)點(diǎn)作為頭結(jié)點(diǎn)的 BST 的種類?共有 dp[j - 1] * dp[i - j] 種!因此,我們只要把「不同頭結(jié)點(diǎn)的 BST 數(shù)量」累加在?起,就能得到 dp[i] 的值: dp[i] += dp[j - 1] * dp[i - j] ( 1 <= j <= i) ?!缸⒁?的是 += ,并且 j 從 1 變化到 i 」。
3. 初始化:
我們注意到,每?個(gè)狀態(tài)轉(zhuǎn)移??的 j - 1 和 i - j 都是?于 i 的,并且可能會(huì)?到前?個(gè)的狀態(tài)(當(dāng) i = 1 , j = 1 的時(shí)候,要?到 dp[0] 的數(shù)據(jù))。因此要先把第?個(gè)元素初始化。當(dāng) i = 0 的時(shí)候,表??顆空樹,「空樹也是?顆?叉搜索樹」,因此 dp[0] = 1 。
4. 填表順序:
根據(jù)「狀態(tài)轉(zhuǎn)移?程」,易得「從左往右」。
5. 返回值:
根據(jù)「狀態(tài)表?」,我們要返回的是 dp[n] 的值。

