關(guān)于我為什么要寫單獨(dú)開一篇文章寫二分,實(shí)際上那么多困難的算法,比如線段樹,并查集等等都沒有難倒我,我最近卻被二分難倒了,而且是兩次,兩次在賽場上做不出來二分的應(yīng)用題,于是我決定寫一篇二分查找的算法總結(jié).剛接觸算法的時(shí)候本來是要寫一篇的,但后面因?yàn)楦鞣N原因擱置了,現(xiàn)在來補(bǔ)一篇.我學(xué)的二分查找和傳統(tǒng)的二分查找有一定的差別.傳統(tǒng)的是將l和r都集中在一個(gè)點(diǎn),這樣非常不好處理邊界.我學(xué)的二分查找會(huì)把l和r處理成相鄰的兩個(gè)元素.看下圖.

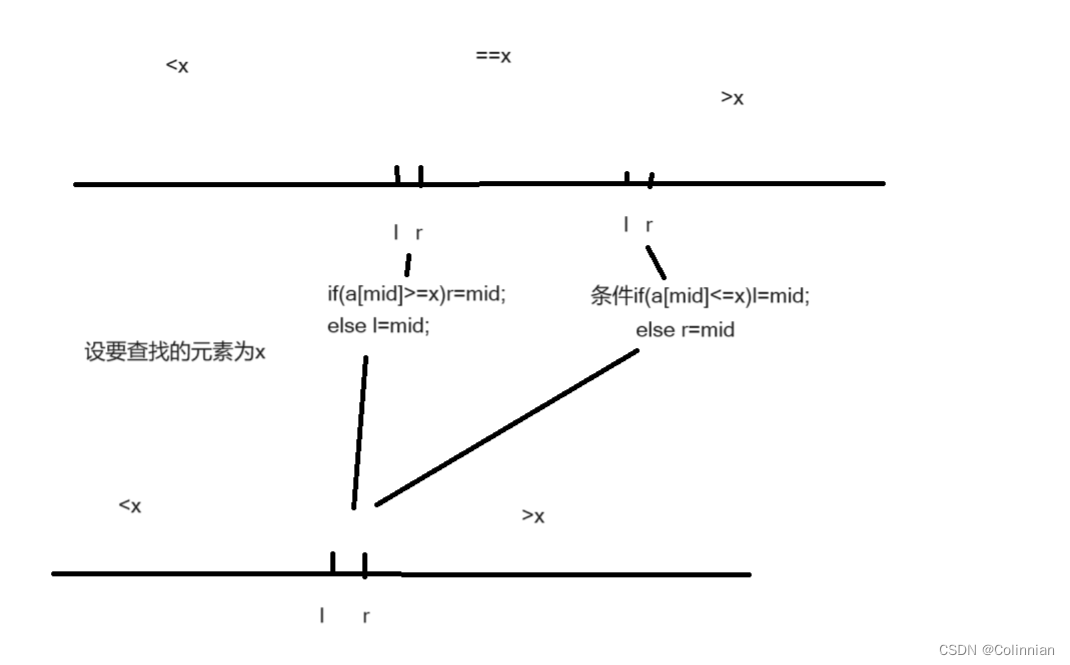
一種是中間有相等元素的情況,一種的沒有的情況,兩個(gè)條件對于第一種會(huì)通向各自所屬情況,這也很好理解,對于第一種,如果mid>=x,你把它賦值給r,那就說明r最后所屬元素肯定時(shí)>=x,而l是<x,它們最終會(huì)出現(xiàn)在各自的邊界.這個(gè)問題解決了,我們來看while循環(huán)里該填什么條件,實(shí)際上應(yīng)該填l+1<r,最終如果l+1==r了就不再進(jìn)行查找了,說明已經(jīng)找到邊界了.

那最初的邊界l和r應(yīng)該怎么定義呢,我們先考慮一種特殊情況,假如<x或>x不存在,l和r該指向哪,對于第一種l是不是指向第一個(gè)元素的左邊呀,r指向第一個(gè)元素,應(yīng)為沒有mid能賦給l,既然l會(huì)出現(xiàn)在第一個(gè)元素的左邊,那我們定義邊界的時(shí)候是不是也要讓它為第一個(gè)元素的左邊?同理r要定義為最右邊的元素的右邊一個(gè),寬泛來講,l定義為要查找范圍最左邊元素的左邊一個(gè)元素,r為要查找范圍的最右邊的元素的右邊一個(gè).

總結(jié)一下

1.while(),括號里填l+1<r.

2.查找第一個(gè)大于等于x的,使用if(a[mid]>=x)r=mid;else l=mid.反之見上面的圖(懶).

3.邊界定義:l定義為要查找范圍最左邊元素的左邊一個(gè)元素,r為要查找范圍的最右邊的元素的右邊一個(gè).

對于基礎(chǔ)練習(xí),這邊建議刷一下洛谷的二分題單,還是很簡單的【算法1-6】二分查找與二分答案 - 題單 - 洛谷

下面我主要想講一下卡了我的一道div3的E題題

Problem - E - Codeforces

沒做出來真羞恥啊?

using i64 = long long;
using ll = long long;
i64 calc(int u, int x) {//x個(gè)跑道,相當(dāng)于u,u-1,u-2...u-x+1,總共有x個(gè),那不就是倒序相加公式嘛return 1LL * (u + u - x + 1) * x / 2;
}
void solve() {ll n;std::cin >> n;std::vector<ll>a(n), b(n + 1);
//維護(hù)前綴和for (int i = 0; i < n; i++) {std::cin >> a[i];b[i + 1] = b[i] + a[i];}ll q, l, u;std::cin >> q;std::vector<ll>bns;while (q--) {std::cin >> l >> u;u;//前面說的邊界問題,找l到n,邊界定義為l-1,n+1l--;ll k = l, j = n + 1;while (l + 1 < j) {ll mid = (l + j) / 2;if (b[mid] < b[k] + u)l = mid;else j = mid;}i64 ans = -1E18;int r = -1;//右邊界小于等于nif (j <= n) {if (calc(u, b[j] - b[k]) > ans) {ans = calc(u, b[j] - b[k]);r = j;}}//j左邊是l,l=j-1,k是l-1,l不能等于k-1,所以j-1>kif (j-1>k) {if (calc(u, b[j - 1] - b[k]) >= ans) {ans = calc(u, b[j - 1] - b[l]);r = j - 1;}}bns.push_back(r);}//其實(shí)你可以直接打印,沒必要像我一樣先存數(shù)組里.for (int i = 0; i < bns.size(); i++)std::cout << bns[i] << ' ';std::cout << '\n';
}
int main() {std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);int t;std::cin >> t;while (t--) {solve();}return 0;
}

實(shí)際上把邊界處理好這道題還是很簡單的,怪我太笨了.