哦我想這不用看都知道是為了水任務(wù)

T1 黑白染色

其實(shí)這題有原

什么手寫體 md (指 markdown)

分析

首先這題如果你題目沒看錯(cuò)的話 ,會(huì)發(fā)現(xiàn)其實(shí)他是 $n\times m$ 讓你求 $n\times n$ 的區(qū)域內(nèi)的點(diǎn)（不會(huì)只有我一個(gè)人題目看錯(cuò)了罷

然后我們會(huì)發(fā)現(xiàn)其實(shí)我們只關(guān)心每一列放了多少，并不關(guān)心是怎么放的（這一步可以用組合數(shù)算出來）

波利亞說過解題時(shí)可以回到定義上去 ， 所以列出公式（這里 $num[i]$ 代表每一列放置點(diǎn)的數(shù)量）
$$\begin{array}{c}{\sum }_{i=1}^{n}num[i]=k\\ {\sum }_{i=2}^{n+1}num[i]=k\end{array}$$

兩式相減就可以得到：$num[i]=num[i+n]$

所以我們就發(fā)現(xiàn)了所有模 $n$ 余數(shù)相同的列的值時(shí)一樣的

剩下的我就不知道了

Code

我講不來但是我有代碼

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define int long long
const int N = 1e6+10;
const int M = 1e5+10;
const int mod = 1e9+7;
using namespace std;
int c[200][200];
int d[200][200];
int dp[200][10005];
int n,m,k;
int ksm(int a, int b){int x = a,ans = 1;while(b){if(b & 1){ans  = ans * x % mod;}x = x * x % mod;b >>= 1;}return ans;
}
signed main(){freopen("discolour.in","r",stdin);freopen("discolour.out","w",stdout);cin >> n >> m >> k;for(int i =1;i <= 100; i++){c[i][0] = c[i][i] = 1;for(int j = 1; j < i; j++){c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod;}}for(int i = 1;i <= n; i++){for(int j = 0; j <= n; j++){d[i][j] = ksm(c[n][j],m/n+(m/n*n+i<=m));
//			cout << d[i][j] << endl;}}dp[0][0] = 1;for(int i = 1; i <= n; i++){for(int j = 0; j <= min(k,n*i); j++){for(int kk = 0; kk <= min(j,n); kk++){dp[i][j] = (dp[i][j] + dp[i-1][j-kk]*d[i][kk] % mod)%mod;
//				cout << dp[i][j] << endl;}}}cout << dp[n][k];return 0;
}

當(dāng)時(shí)還把 colour 打成了 color , 幸好最后改回來了

cspj的時(shí)候文件保存按成了撤銷痛失100分我不說是誰

T2 造城墻

有一說一這題數(shù)據(jù)是真的弱啊

首先，對(duì)于 $40\%$ 的數(shù)據(jù)，可以直接狀壓

然后對(duì)于另外 $20\%$ 的數(shù)據(jù)可以直接染色跑二分圖

分析

正文開始

看到這題其實(shí)像 czy 那樣的猥瑣小子大佬，第一反應(yīng)應(yīng)該就是網(wǎng)絡(luò)流罷，對(duì)棋盤黑白染色，這個(gè)應(yīng)該不難想

沒錯(cuò)這個(gè)跟這道題的正解沒關(guān)系
但是可以幫助你理解思路

注意下面均用 0 代表偶數(shù) 1 代表奇數(shù)

首先一個(gè)很顯然的貪心就是 所有橫著的磚塊肯定放在最頂上

如果你用腳造了幾組數(shù)據(jù)玩玩的話你會(huì)發(fā)現(xiàn)，所有橫著放的磚塊會(huì)構(gòu)成多個(gè)倒三角

like this

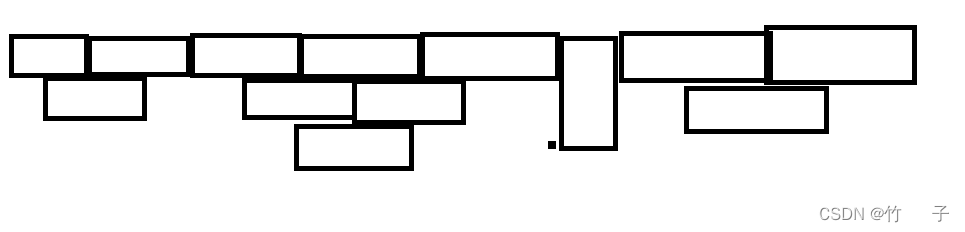
如果對(duì)于這個(gè)倒三角還有點(diǎn)懵的可以在這里停一下搞清楚先

所以我們考慮維護(hù)當(dāng)前列倒三角的高度

讓我們隨便造幾組數(shù)據(jù)（下面的數(shù)據(jù)均是空白格的個(gè)數(shù)）
一列一列枚舉：1 高度為 1， 10 高度為 2 ， 101 高度為 3，1011 高度為3 ， 10110 高度為2

這里發(fā)現(xiàn)什么，當(dāng)出現(xiàn) 00 或者 11 的時(shí)候高度不會(huì)再增加，并且下一行如果奇偶性不同高度還會(huì)減 1 （其實(shí)這個(gè)應(yīng)該看圖就知道了罷

如果您無法理解

可以把他看成一個(gè)黑白染色，每一列不能匹配的黑格子都會(huì)被放到最頂上，這樣一列一列的黑格子剩下來就是高度了

那接下來就考慮維護(hù)高度，有了上面的規(guī)律之后，我們記 $black$ 為當(dāng)前的高度（黑格子數(shù)）

不難發(fā)現(xiàn)，如果當(dāng)前的空白格數(shù)小于黑格子數(shù)，肯定就不能滿足。如果空白格數(shù)減黑格子數(shù)為奇數(shù)，那黑格子數(shù)就要加一，如果為偶數(shù)，那就減一

最后別忘了在黑格子減一的時(shí)候和 0 取 $max$ （其實(shí)不取你也能得到 80 分的好成績(jī)）

Code

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define int long long
const int N = 1e6+10;
const int M = 1e5+10;using namespace std;
int n;
priority_queue<pair<int,int>,vector<pair<int,int> > , greater<pair<int,int> > > q;
int x,y,z;signed main(){freopen("chicken.in","r",stdin);freopen("chicken.out","w",stdout);cin >> n;cin >> x >> y >> z;int t,a;cin >> t >> a;q.push(make_pair(t-z+y,a));int sum = a;for(int i = 2; i <= n; i++){cin >> t >> a;while(a){int xx = q.top().first,num = q.top().second;if(xx + x <= t){
//				cout << xx << " " << num << endl;q.pop();if(num > a){num -= a;q.push(make_pair(xx,num));q.push(make_pair(max(xx+x+z,t-y+z),a));a = 0;}else{a -= num;q.push(make_pair(max(xx+x+z,t-y+z),num));}
//			cout << xx << " xx ";
//				cout << max(xx+x+y,t-z+y) << " xx ";}else{q.push(make_pair(t-y+z,a));
//				cout << t-y+z << " " << a << endl;sum += a;a = 0;
//				cout << t-z+y << " yy ";}}
//		cout << endl;}cout << sum;return 0;
}

T3 炸雞

這手寫的 $\text{LATE?X}$ 是真的一言難盡

分析

這題有一個(gè)很重要的性質(zhì)就是 ：同一份訂單中，不會(huì)有任何一口鍋?zhàn)龀^一份的雞（因?yàn)殡u的保存時(shí)間小于制作時(shí)間）

接下來考慮貪心

雖然我們是非常單純美好的，但是這題的做法非常的黑心，那就是 給顧客的雞能多接近保質(zhì)期就多接近保質(zhì)期

然后我們就可以用優(yōu)先隊(duì)列維護(hù)每口鍋?zhàn)钤玳_始的閑置時(shí)間，然后每次取最早的就行，如果沒有鍋滿足要求那就新買幾口鍋 為了讓顧客吃上臨近保質(zhì)期的雞我還新買鍋我真是太偉大了)

寫代碼的時(shí)候記得搞清楚每口鍋?zhàn)钤玳_始閑置的時(shí)間是什么

好的我們寫完了這個(gè)非常czy的代碼，定睛一看，忽然發(fā)現(xiàn)，數(shù)據(jù)范圍是$10^9$ 而不是 10

那這樣我們一個(gè)一個(gè)丟肯定不對(duì)，那么怎么辦呢？
如果你把每次取出的鍋的時(shí)間都輸出來，你會(huì)發(fā)現(xiàn)，有很多鍋的時(shí)間其實(shí)是一樣的
（別問我為什么要輸出，因?yàn)楫?dāng)時(shí)把 $y,z$ 看反了）

這樣想到什么？ 沒錯(cuò)往堆里面丟 $pair$ 不就好了嗎

Code

這里有個(gè)小技巧就是一開始就把第一次所用的鍋都扔進(jìn)去，這樣可以防止越界和代碼打漏

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define int long long
const int N = 1e6+10;
const int M = 1e5+10;using namespace std;
int n;
priority_queue<pair<int,int>,vector<pair<int,int> > , greater<pair<int,int> > > q;
int x,y,z;signed main(){freopen("chicken.in","r",stdin);freopen("chicken.out","w",stdout);cin >> n;cin >> x >> y >> z;int t,a;cin >> t >> a;q.push(make_pair(t-z+y,a));int sum = a;for(int i = 2; i <= n; i++){cin >> t >> a;while(a){int xx = q.top().first,num = q.top().second;if(xx + x <= t){
//				cout << xx << " " << num << endl;q.pop();if(num > a){num -= a;q.push(make_pair(xx,num));q.push(make_pair(max(xx+x+z,t-y+z),a));a = 0;}else{a -= num;q.push(make_pair(max(xx+x+z,t-y+z),num));}
//			cout << xx << " xx ";
//				cout << max(xx+x+y,t-z+y) << " xx ";}else{q.push(make_pair(t-y+z,a));
//				cout << t-y+z << " " << a << endl;sum += a;a = 0;
//				cout << t-z+y << " yy ";}}
//		cout << endl;}cout << sum;return 0;
}

T4 騎士與國王

這題其實(shí)就是個(gè)容斥對(duì)吧（逃)

Code

我這題沒打，那就放一下 $xhgua?hyx$ 大帝的代碼罷

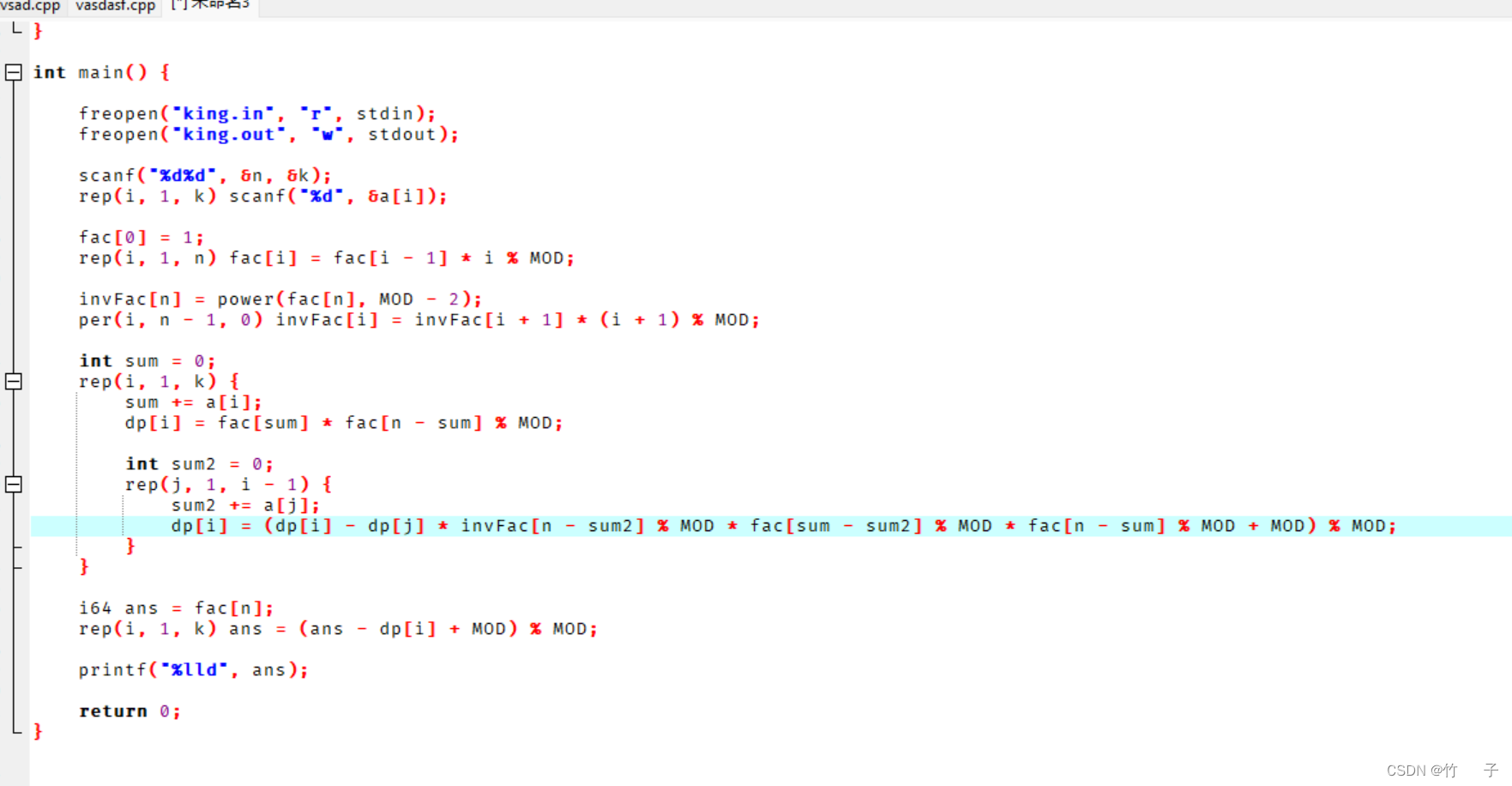
黃瓜好吃，拜謝黃瓜！！！

結(jié)語

誰家 noip 3道數(shù)學(xué)題起步啊

誰家 noip 3小時(shí)不到啊

誰家 noip 有人踹電源線啊

有一說一 OI這玩意真的運(yùn)氣成分很高

$$\begin{array}{c}我愛優(yōu)先隊(duì)列!\\ 優(yōu)先隊(duì)列好閃拜謝優(yōu)先隊(duì)列！！！\\ 以后找對(duì)象就找優(yōu)先隊(duì)列這樣的!!!\end{array}$$