1.消失的數(shù)字

【題目】：題目鏈接

思路1：排序——》qsort快排——》時間復雜度O（n*log2n）? 不符合要求

思路2：（0+1+2+3+...+n)-(a[0]+a[1]+[2]+...+a[n-2]) ——》

時間復雜度O（N）空間復雜度為O（1）

（0+1+2+3+...+n)直接用等差數(shù)列求和就可

思路3：數(shù)組中是幾就在第幾個位置寫一下這個值? ——》時間空間復雜度都為O（N）

思路4：給一個值x=0，

x先跟[0,n]的所有值異或，

x再跟數(shù)組中的每個值異或，最后x就是缺的那個數(shù)字

（異或的特點相同的數(shù)異或為0，0跟一個數(shù)異或為這個數(shù)，且異或滿足交換律）

時間復雜度O（N） 空間復雜度O（1）

eg：假設[0,9]缺一個8，先讓x=0跟[0,9]不缺8的數(shù)一個一個異或（0跟一個數(shù)異或為這個數(shù)，這樣初始化以后就不會被x所影響），異或完的結(jié)果還是[0,9],然后這些值和缺8的數(shù)組異或，結(jié)果發(fā)現(xiàn)這兩個數(shù)組中相同的兩個數(shù)異或為0就沒了（可以直接交換律理解），最后只剩下0和8異或，異或結(jié)果就是8（也就是缺少的數(shù)字）

【圖解】：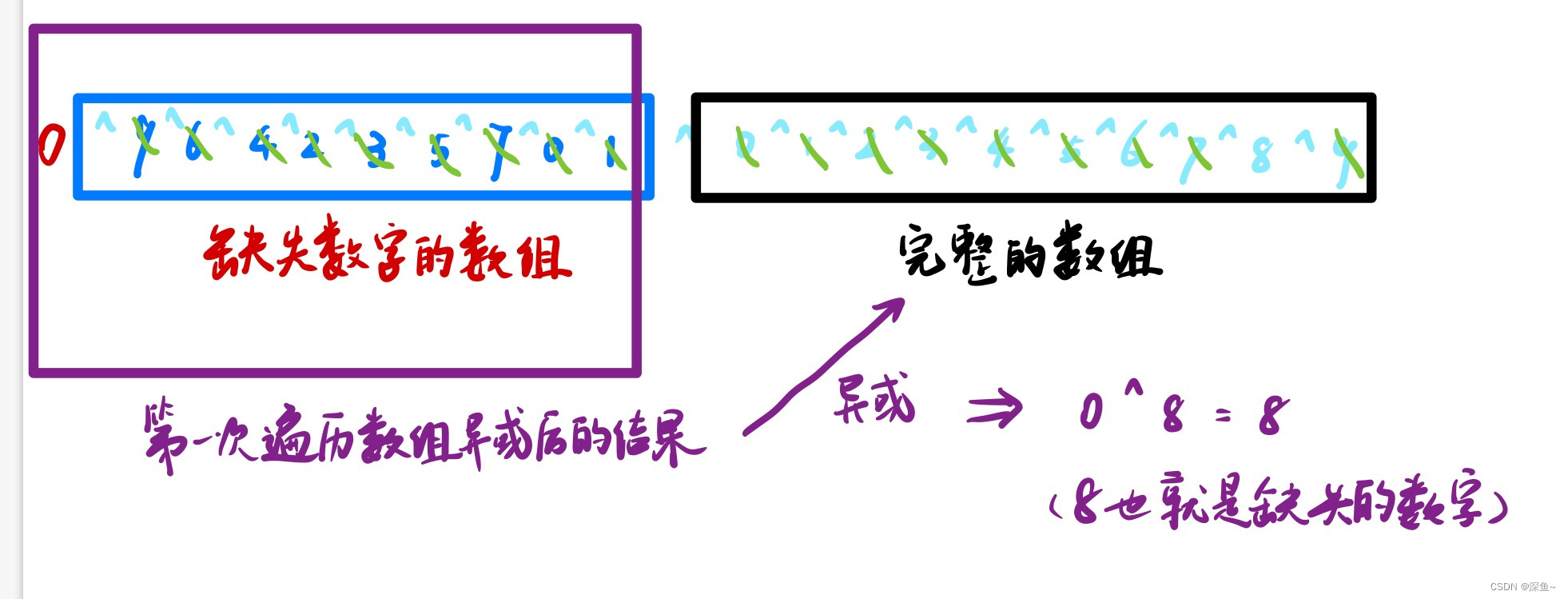

?本題推薦思路2和思路4：時間空間復雜度最優(yōu)

思路2代碼實現(xiàn)：

int missingNumber(int* nums, int numsSize)
{//等差數(shù)列求和int sum=((1+numsSize)*numsSize)/2;//sum減去數(shù)組中的元素for(int i=0;i<numsSize;i++){sum-=nums[i];}return sum;
}

思路4代碼實現(xiàn)：

int missingNumber(int* nums, int numsSize){int x=0;//跟數(shù)組中的值異或for(int i=0;i<numsSize;i++)//這里少一個數(shù)，直接<{x^=nums[i];}//跟[0,9]的值異或for(int i=0;i<=numsSize;i++)//這里多一個數(shù)（n+1）個，<={x^=i;}return x;
}

2.旋轉(zhuǎn)數(shù)組

【題目】：題目鏈接

?

?思路1：暴力求解，旋轉(zhuǎn)K次（一次一次地移，直到旋轉(zhuǎn)

時間復雜度：O（N*K）空間復雜度：O（1）

思路2：開辟額外空間，以空間換時間

（創(chuàng)建一個數(shù)組，要移動到前面的就放入數(shù)組，其他部分向后移動即可）

時間復雜度：O（N） 空間復雜度：O（N）

思路3：（1）前n-k個數(shù)字逆置

? ? ? ? ? ? ? （2）后k個逆置

? ? ? ? ? ? ? ?（3）整體逆置

時間復雜度：O（N） 空間復雜度：O（1）

這里肯定是思路3最優(yōu)

代碼演示：

void reverse(int *nums,int left,int right)
{while(left<right){int tmp=nums[left];nums[left]=nums[right];nums[right]=tmp;left++;right--;}
}
void rotate(int* nums, int numsSize, int k)
{k=k%numsSize;//倒置前n-k個數(shù)字reverse(nums,0,numsSize-k-1);//倒置后k個數(shù)字reverse(nums,numsSize-k,numsSize-1);//倒置整個數(shù)組reverse(nums,0,numsSize-1);
}

k=k%numsSize;的意思就是如果k的大小大于numsSize的大小，那么就需要對k進行取模操作，這樣避免重復操作，效率更高

本次數(shù)據(jù)結(jié)構(gòu)時間空間復雜度練習的內(nèi)容就到此啦，有什么問題歡迎評論區(qū)或者私信交流，覺得筆者寫的還可以，或者自己有些許收獲的，麻煩鐵汁們動動小手，給俺來個一鍵三連，萬分感謝 !?