題目鏈接
好久沒有寫題了復(fù)健一下qwq

題目大意

解題思路

這題目還挺妙的
首先考慮比較正常的dp，$dp[i][j]$ 為前$i$的長度選$j$個(gè)長度的最大價(jià)值，那么轉(zhuǎn)移方程是：
圖片來自：圖片來源

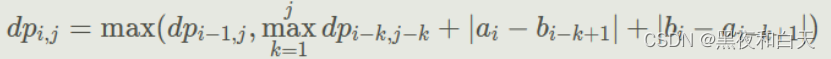
但是這個(gè)是$O(n{k}^2)$無法通過把絕對值展開進(jìn)行討論

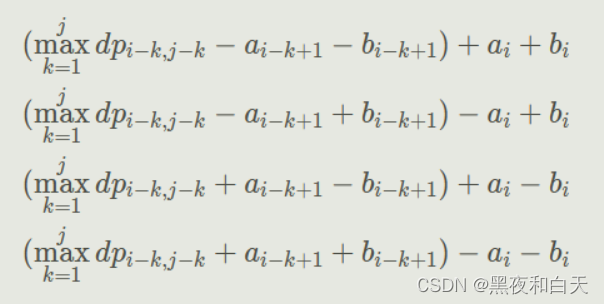
• 我們可以看到$dp[i][j]$其實(shí)都是由對角線上的$dp$值$+$幾個(gè)$a$,$b$的計(jì)算，那么我們可以把前面的部分用新的數(shù)組維護(hù)起來因?yàn)槎际菍巧系臄?shù)值那么$i?j$是固定值那么就是$f[0/1/2/3][i?j]$里面取最大值$+$后綴部分
• 然后因?yàn)檫@個(gè)雖然是對角線的上值的前$k$里面的最大值，但是其實(shí)$dp[i][j]>dp[i?1][j?1]$是一定成立的所以$f[0/1/2/3][i?j]$只用從$k=1$轉(zhuǎn)移就行

				f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);f[1][i - j] = std::max(f[1][i - j], dp[i - 1][j - 1] + a[i] - b[i]);f[2][i - j] = std::max(f[2][i - j], dp[i - 1][j - 1] - a[i] + b[i]);f[3][i - j] = std::max(f[3][i - j], dp[i - 1][j - 1] + a[i] + b[i]);

• 記住f數(shù)組要初始化為負(fù)無窮，不能是0

memset(f,0x80,sizeof(f));

• 整體代碼

#include <iostream>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 3005;
typedef long long ll;
const ll mod = 998244353;
int a[maxn], b[maxn];
ll dp[maxn][maxn], f[4][maxn]; 
int main() {//freopen("1.txt","r",stdin);int T;scanf("%d",&T);while(T --) {int n, k;scanf("%d%d",&n,&k);memset(f,0x80,sizeof(f));// 這個(gè)0x80初始化出來是復(fù)數(shù) for(int i = 1; i <= n; ++ i) cin >> a[i];for(int i = 1; i <= n; ++ i) cin >> b[i]; for(int i = 1; i <= n; ++ i) {for(int j = 1; j <= k && j <= i; ++ j) {dp[i][j] = dp[i-1][j];f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);f[1][i - j] = std::max(f[1][i - j], dp[i - 1][j - 1] + a[i] - b[i]);f[2][i - j] = std::max(f[2][i - j], dp[i - 1][j - 1] - a[i] + b[i]);f[3][i - j] = std::max(f[3][i - j], dp[i - 1][j - 1] + a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[0][i - j] + a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[1][i - j] + a[i] - b[i]);dp[i][j] = std::max(dp[i][j], f[2][i - j] - a[i] + b[i]);dp[i][j] = std::max(dp[i][j], f[3][i - j] - a[i] - b[i]);
//                for(int h = 1; h <= j; ++ h) {
//                    dp[i][j] = max(dp[i-h][j-h]+abs(a[i]-b[i-h+1])+abs(a[i-h+1]-b[i]),dp[i][j]);
//                    // printf("%d %d %lld\n",i,j,dp[i][j]);
//                }}}printf("%lld\n",dp[n][k]);} return 0;
}

• 上面你可能會(huì)疑問這個(gè)不是抵消了嗎？

f[0][i - j] = std::max(f[0][i - j], dp[i - 1][j - 1] - a[i] - b[i]);
dp[i][j] = std::max(dp[i][j], f[0][i - j] + a[i] + b[i]);

注意其實(shí)這里的有個(gè)影響是$f[0][i?j]$是包含了帶$k$的參數(shù) 所以要做兩次$max$,$dp[i?1][j?1]?a[i]?b[i]$只是剛好這一層兒而已