算法流程：?

1. 與?結(jié)點的權(quán)值作?較，如果?它?，就與?親交換；?
2. 交換完之后，重復(fù) 1 操作，直到??親?，或者換到根節(jié)點的位置

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

這里為什么插入85完后合法？

我們插入一個85，當(dāng)85還沒來的時候，此時的堆是一個合法的大堆，所有的節(jié)點都大于等于子樹中所有節(jié)點，85到來的時候，我會拿它和它的父節(jié)點作比較，如果它小于父結(jié)點，比如3，那就不用調(diào)整，因為當(dāng)前節(jié)點小于父節(jié)點，也肯定小于父節(jié)點的父結(jié)點，因為這是一個堆結(jié)構(gòu)，只要他小于父結(jié)點，他肯定小于沿著這個節(jié)點向上的所有節(jié)點，因此在3到來的時候它還是合法的；但是當(dāng)85到來的時候，85的值大于22，因此我會讓較大的值往上轉(zhuǎn)移，轉(zhuǎn)移完之后下面的堆就合法了，85是大于22的，因為22大于左子樹數(shù)，所以我把較大的值挪下來之后，85肯定大于下面兩顆子樹里面所有的節(jié)點，因此85轉(zhuǎn)移下來之后，下面的小樹就合法了

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

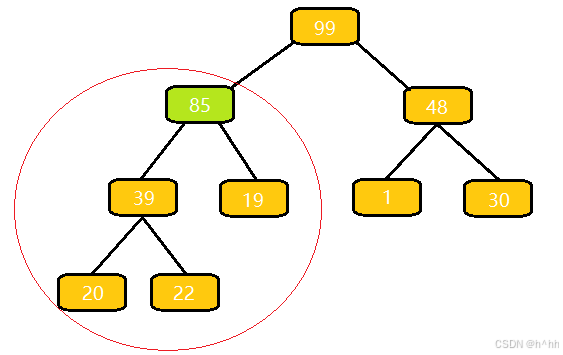
但是上面的我們還不確定，所以我們要繼續(xù)拿85和上面的點做比較，當(dāng)我們發(fā)現(xiàn)85比39還大的時候就繼續(xù)轉(zhuǎn)移，轉(zhuǎn)移完之后下面的子樹依舊是合法的，因為39沒轉(zhuǎn)移之前是大于它的左子樹和右子樹里面所有的點，所以當(dāng)我把39轉(zhuǎn)移到下面的時候，他依舊是大于20和22這兩個點的，把39轉(zhuǎn)移到下面的子樹是不受影響的，但是當(dāng)我把85轉(zhuǎn)移到上面的紅圈中的子樹就合法了，原因就是剛剛85是比39大的，85轉(zhuǎn)移到上面之后，85肯定是大于剛剛左子樹里面所有的節(jié)點，以及剛剛右子樹里面所有的節(jié)點，因為39放在這里就合法，那我把85放在這里也是合法的，因此當(dāng)我把85轉(zhuǎn)移到上面的時候，整顆子樹就變得合法了，每次向上轉(zhuǎn)移，他都會讓一顆小子樹合法，繼續(xù)向上轉(zhuǎn)移，又會讓一顆小子樹合法，此時我們發(fā)現(xiàn)85比99小，左邊的子樹就合法了，右邊的子樹本身就是合法的，因為85到來的時候并不會影響右子樹，85向上調(diào)整的時候，他會讓一個小子樹再讓一顆小子樹變得合法，因此整個指數(shù)就變得合法了，所以這里為什么合法，就是一個簡單比大小的過程，一直讓大的元素向上再向上，上到不能再上的時候整個數(shù)就合法了，這就是堆的第一個核心操作向上調(diào)整算法，如果是小堆的話，就讓小元素向上走

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

向上調(diào)整算法時間復(fù)雜度

最壞情況下節(jié)點會從最后一層開始轉(zhuǎn)移上一層，再轉(zhuǎn)移上一層，所以他向上轉(zhuǎn)移的次數(shù)跟樹的高度是一樣的，在我們學(xué)習(xí)完全二叉樹性質(zhì)的時候，當(dāng)整棵樹節(jié)點個數(shù)為N的話，它的樹的高度是loh以2為底N +1的對數(shù)，時間復(fù)雜度就是O（logN）

代碼實現(xiàn)：

const int N = 1e6 + 10;int n;
int heap[N];//向上調(diào)整算法
void up(int child) //每次和父親做比較
{int parent = child / 2;//父節(jié)點存在且當(dāng)前結(jié)點值大于父節(jié)點的權(quán)值while (parent >= 1 && heap[child] > heap[parent]){swap(heap[child], heap[parent]);child = parent;parent = child / 2;}
}

• 這個向上調(diào)整算法是為建堆服務(wù)的，對我們建完堆之后再來測試