合肥建站企業(yè)百度指數(shù)的數(shù)據(jù)怎么導(dǎo)出
🦄個人主頁:修修修也
🎏所屬專欄:數(shù)據(jù)結(jié)構(gòu)
??操作環(huán)境:Visual Studio 2022

算法空間復(fù)雜度的定義
算法的時間復(fù)雜度和空間復(fù)雜度是度量算法好壞的兩個重要量度,在實際寫代碼的過程中,我們完全可以用空間來換時間,比如說,我們要判斷某某年是不是閏年,大家可能第一時間想到的都是寫一個算法來判斷每次輸入的年份符不符合閏年的條件.但其實還有種方法是,我們可以事先建立一個有2050個元素的數(shù)組(年數(shù)比現(xiàn)實略多一點),然后把所有年份按下標(biāo)數(shù)字對應(yīng),如果是閏年,此數(shù)組項的值設(shè)為1,否則設(shè)為0.這樣,判斷某年是否是閏年,就只需要查找一下對應(yīng)數(shù)組項的值就可以了.這樣求閏年的時間復(fù)雜度為O(1).既然空間復(fù)雜度這么好用,接下來我們就來一起學(xué)習(xí)它的基本內(nèi)容吧.
上篇文章中我們一起探討了算法的時間復(fù)雜度的相關(guān)知識,在這節(jié)我們將一起探討算法的空間復(fù)雜度的相關(guān)知識.
先來看算法空間復(fù)雜度的定義:
算法的空間復(fù)雜度通過計算算法所需的存儲空間實現(xiàn),算法空間復(fù)雜度的計算公式記作:S(n)=O(f(n)).
其中,n為問題的規(guī)模,f(n)為語句關(guān)于n所占存儲空間的函數(shù).
通過上節(jié)對時間復(fù)雜度的分析可知,算法的時間復(fù)雜度不是用來計算程序具體耗時的,同樣的,空間復(fù)雜度也不是用來計算程序?qū)嶋H占用的空間的.
空間復(fù)雜度是對一個算法在運行過程中臨時占用存儲空間大小的一個量度,同樣反映的是一個趨勢,我們用S(n)來定義.
空間復(fù)雜度計算規(guī)則基本跟時間復(fù)雜度類似,也使用大O漸近表示法.
注意:函數(shù)運行時所需要的??臻g(存儲參數(shù),局部變量,一些寄存器信息等)在編譯期間已經(jīng)確定好了,因此空間復(fù)雜度主要通過函數(shù)在運行時侯顯示申請的額外空間來確定.
一般情況下,算法要占據(jù)的空間可以分為兩部分:
- 算法本身要占據(jù)的空間,輸入和輸出,指令,常數(shù),變量等.
- 算法要使用的輔助空間.
第一條大家應(yīng)該很好理解,一個程序在機(jī)器上執(zhí)行時,需要存儲程序本身的指令,常數(shù),變量和輸入數(shù)據(jù).
除此之外,還需要存儲對數(shù)據(jù)操作的存儲單元,對數(shù)據(jù)操作的存儲單元即算法的輔助空間.
我們參照一個實際程序(冒泡排序函數(shù))來理解一下這個概念:
//冒泡排序函數(shù)
void bubbleSort(int arr[], int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){// 交換arr[j]和arr[j+1]int temp = arr[j]; //變量temp占據(jù)的空間就是輔助空間arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}如上,在冒泡排序函數(shù)中,我們需要開辟一個整形變量temp,它占據(jù)4個字節(jié),這4個字節(jié)的空間就是冒泡排序算法在運行過程中要使用的輔助空間.
至于其他的變量i,j或是數(shù)組arr,則都屬于算法本身要占據(jù)的空間,即無論使不使用冒泡排序算法程序運行都要使用的空間.這部分空間不計入算法空間復(fù)雜度的度量.
常見的空間復(fù)雜度
📌常數(shù)階
如果算法執(zhí)行所需要的臨時空間不隨著某個變量n的大小而變化,即此算法空間復(fù)雜度為一個常量,可表示為O(1).
再拿上面的冒泡排序舉例:
//冒泡排序函數(shù)
void bubbleSort(int arr[], int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){// 交換arr[j]和arr[j+1]int temp = arr[j]; //變量temp每次進(jìn)入if語句創(chuàng)建,出if語句銷毀arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}可以看到,算法在運行過程中,雖然會循環(huán)很多次交換arr[j]和arr[j+1]的操作,但在這過程中創(chuàng)建的變量temp每次都是進(jìn)入if語句后被創(chuàng)建,出if語句后被銷毀,因此即便創(chuàng)建temp的語句運行的次數(shù)隨n的增大在不斷變多,但其本質(zhì)上用的都是同一塊空間,不論n大小如何變化,temp占用的空間大小都不會變化,因此冒泡排序的空間復(fù)雜度為O(1).
📌線性階
如果算法執(zhí)行所需要的臨時空間隨著某個變量n的大小呈線性變化,即此算法空間復(fù)雜度為一個線性階,可表示為O(n).
假設(shè)我們現(xiàn)在要求出從0開始的n個素數(shù),將它們存儲在數(shù)組arr中,代碼如下:
int main()
{int i, j,k, flag;int n; int arr[n] = { 0 }; //僅作示例演示,正式編程時變量不能作為數(shù)組長度for (i = 0; k < n; i++){flag = 1;for (j = 2; j < i; j++){if (i % j == 0){flag = 0;break;}}if (flag == 1){arr[k] = i;k++;}}return 0;
}在這個程序中我們就需要開辟長度為n的數(shù)組來存放我們求得的n個素數(shù).顯而易見,開辟的數(shù)組長度n是隨著問題規(guī)模的n增長而增長的,且呈線性相關(guān),因此該程序的空間復(fù)雜度為O(n).
常見的時間復(fù)雜度及其耗費空間排序
| 執(zhí)行次數(shù)函數(shù) | 階 | 非正式術(shù)語 |
|---|---|---|
| 5201314 | O(1) | 常數(shù)階 |
| 2n+3 | O(n) | 線性階 |
| 3n^2+2n+1 | O(n^2) | 平方階 |
| O(logn) | 對數(shù)階 | |
| O(nlogn) | nlogn階 | |
| 6n^3+2n^2+3n+4 | O(n^3) | 立方階 |
| 2^n | O(2^n) | 指數(shù)階 |
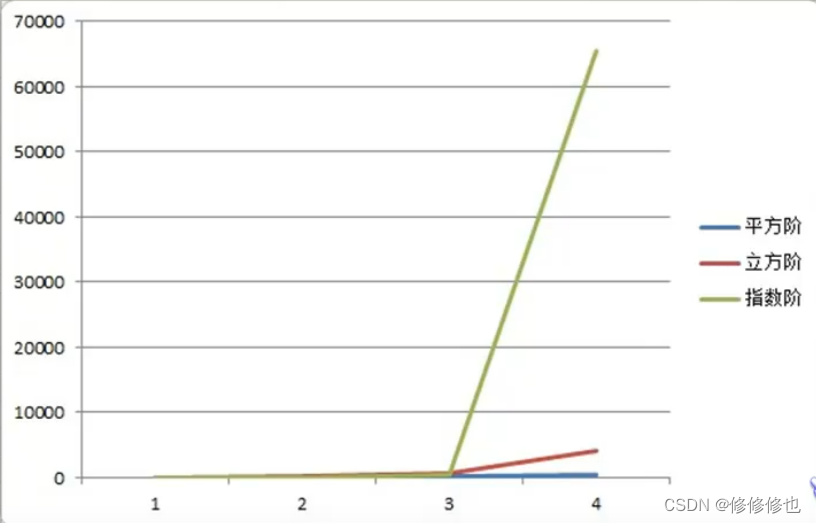
常用的空間復(fù)雜度所耗費的空間從小到大依次是:
 ?
?
結(jié)語
當(dāng)我們搞清楚算法的空間復(fù)雜度后,數(shù)據(jù)結(jié)構(gòu)算法篇的內(nèi)容就結(jié)束了,接下來我們將開啟數(shù)據(jù)結(jié)構(gòu)新的章節(jié)——線性表,在新章節(jié)中我們將一起學(xué)習(xí)如何實現(xiàn)順序表,單鏈表,雙鏈表,循環(huán)鏈表等相關(guān)知識.希望這些內(nèi)容能對大家有所幫助,一起學(xué)習(xí),一起進(jìn)步!
相關(guān)文章推薦
【數(shù)據(jù)結(jié)構(gòu)】什么是數(shù)據(jù)結(jié)構(gòu)?
【數(shù)據(jù)結(jié)構(gòu)】什么是算法?
【數(shù)據(jù)結(jié)構(gòu)】算法效率的度量方法
【數(shù)據(jù)結(jié)構(gòu)】算法的時間復(fù)雜度
【C語言】冒泡排序
【數(shù)據(jù)結(jié)構(gòu)】什么是線性表?
......

數(shù)據(jù)結(jié)構(gòu)算法篇思維導(dǎo)圖: