怎么樣建設(shè)一個(gè)電影網(wǎng)站友情鏈接網(wǎng)自動(dòng)收錄
目錄
1.樹形結(jié)構(gòu)
1.概念
2.二叉樹
2.1概念
2.2 兩種特殊的二叉樹
2.3二叉樹的存儲(chǔ)
2.4二叉樹的基本操作
1.手動(dòng)快速創(chuàng)建一棵簡(jiǎn)單的二叉樹
2.二叉樹的遍歷 (遞歸)
3.二叉樹的層序遍歷
4.獲取樹中節(jié)點(diǎn)的個(gè)數(shù)
5.獲取葉子節(jié)點(diǎn)的個(gè)數(shù)
6.獲取第K層節(jié)點(diǎn)的個(gè)數(shù)
7.獲取二叉樹的高度
8.檢測(cè)值為value的元素是否存在
9.判斷一棵樹是不是完全二叉樹
????????
1.樹形結(jié)構(gòu)
1.概念
????????樹是一種非線性的數(shù)據(jù)結(jié)構(gòu)
????????有一個(gè)特殊的結(jié)點(diǎn),稱為根結(jié)點(diǎn),根結(jié)點(diǎn)沒有前驅(qū)結(jié)點(diǎn)
? ? ? ??每棵子樹的根結(jié)點(diǎn)有且只有一個(gè)前驅(qū),可以有0個(gè)或多個(gè)后繼
????????樹是遞歸定義的
注意:樹形結(jié)構(gòu)中,子樹之間不能有交集,否則就不是樹形結(jié)構(gòu)
結(jié)點(diǎn)的度:當(dāng)前節(jié)點(diǎn)子樹的個(gè)數(shù);
樹的度:最大的結(jié)點(diǎn)的度;
葉子結(jié)點(diǎn)或終端結(jié)點(diǎn):度為0的結(jié)點(diǎn)稱為葉結(jié)點(diǎn)
父結(jié)點(diǎn):若一個(gè)結(jié)點(diǎn)含有子結(jié)點(diǎn),則這個(gè)結(jié)點(diǎn)稱為其子結(jié)點(diǎn)的父結(jié)點(diǎn);
子結(jié)點(diǎn):一個(gè)結(jié)點(diǎn)含有的子樹的根結(jié)點(diǎn)稱為該結(jié)點(diǎn)的子結(jié)點(diǎn);
根結(jié)點(diǎn):沒有前驅(qū)的結(jié)點(diǎn)
結(jié)點(diǎn)的層次:從根開始定義起,根為第1層,根的子結(jié)點(diǎn)為第2層,以此類推
樹的高度或深度:樹中結(jié)點(diǎn)的最大層次;
2.二叉樹
2.1概念
1. 二叉樹不存在度大于2的結(jié)點(diǎn)
2. 二叉樹的子樹有左右之分,次序不能顛倒,因此二叉樹是有序樹
2.2 兩種特殊的二叉樹
1. 滿二叉樹: 一棵二叉樹,如果每層的結(jié)點(diǎn)數(shù)都達(dá)到最大值,則這棵二叉樹就是滿二叉樹。也就是說,如果一棵 二叉樹的層數(shù)為K,且結(jié)點(diǎn)總數(shù)是 2^k - 1,則它就是滿二叉樹。
2. 完全二叉樹: 完全二叉樹是效率很高的數(shù)據(jù)結(jié)構(gòu),完全二叉樹是由滿二叉樹而引出來的。對(duì)于深度為K的,有n 個(gè)結(jié)點(diǎn)的二叉樹,當(dāng)且僅當(dāng)其每一個(gè)結(jié)點(diǎn)都與深度為K的滿二叉樹中編號(hào)從0至n-1的結(jié)點(diǎn)一一對(duì)應(yīng)時(shí)稱之為完全二叉樹
2.3二叉樹的存儲(chǔ)
二叉樹的存儲(chǔ)結(jié)構(gòu)分為:順序存儲(chǔ)和類似于鏈表的鏈?zhǔn)酱鎯?chǔ)。
二叉樹的鏈?zhǔn)酱鎯?chǔ)是通過一個(gè)一個(gè)的節(jié)點(diǎn)引用起來的,常見的表示方式有二叉和三叉表示方式,具體如下
// 孩子表示法
class Node {
int val; // 數(shù)據(jù)域
Node left; // 左孩子的引用,常常代表左孩子為根的整棵左子樹
Node right; // 右孩子的引用,常常代表右孩子為根的整棵右子樹
}
// 孩子雙親表示法
class Node {
int val; // 數(shù)據(jù)域
Node left; // 左孩子的引用,常常代表左孩子為根的整棵左子樹
Node right; // 右孩子的引用,常常代表右孩子為根的整棵右子樹
Node parent; // 當(dāng)前節(jié)點(diǎn)的根節(jié)點(diǎn)
}2.4二叉樹的基本操作
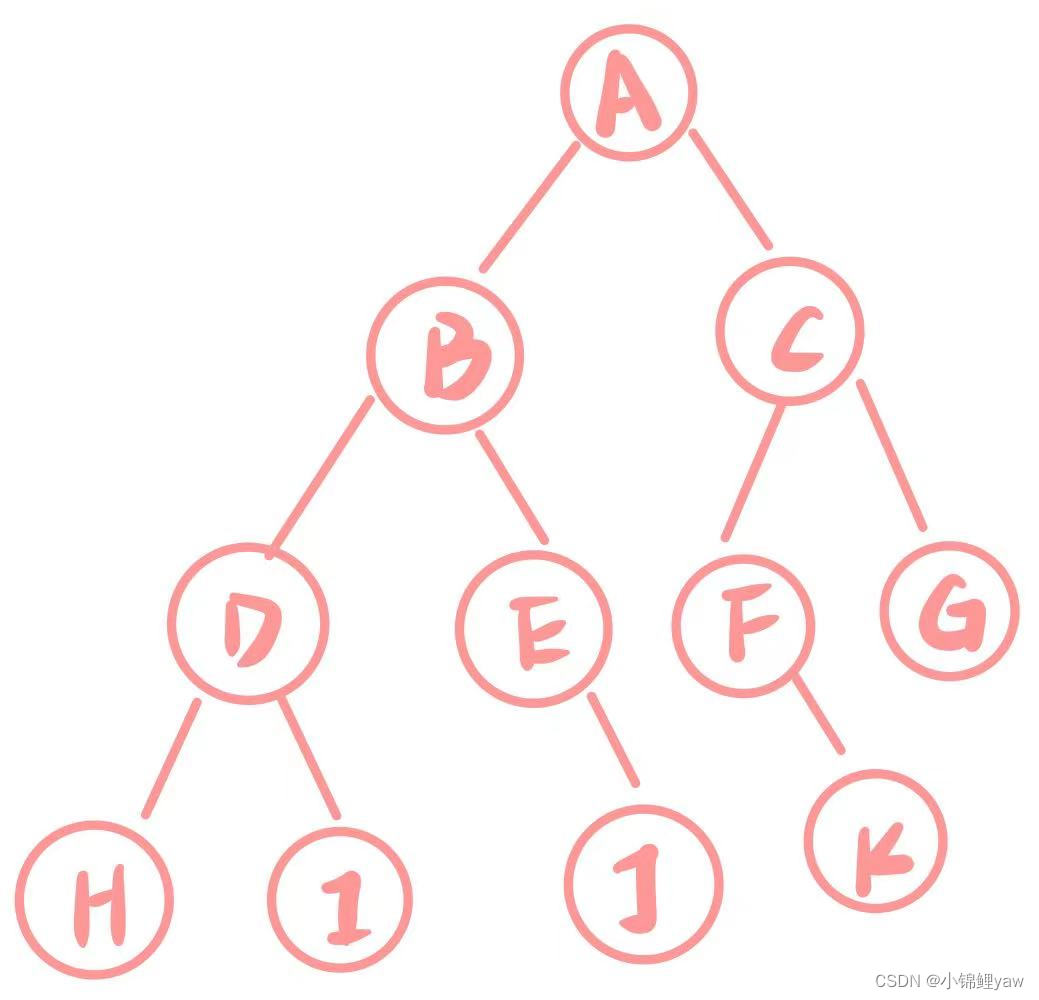
1.手動(dòng)快速創(chuàng)建一棵簡(jiǎn)單的二叉樹
?
public Node TreeBuild(){Node node1 = new Node('A');Node node2 = new Node('B');Node node3 = new Node('C');Node node4 = new Node('D');Node node5 = new Node('E');Node node6 = new Node('F');Node node7 = new Node('G');Node node8 = new Node('H');Node node9 = new Node('I');Node node10 = new Node('J');Node node11 = new Node('K');node1.left = node2;node1.right = node3;node2.left = node4;node2.right = node5;node3.left = node6;node3.right = node7;node4.left = node8;node4.right = node9;node5.right = node10;node6.right = node11;return node1;}2.二叉樹的遍歷 (遞歸)
· //前序遍歷public void preOrder(Node root){if(root == null){return ;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}//中序遍歷public void inOrder(Node root){if(root == null){return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}//后序遍歷public void postOrder(Node root){if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}
3.二叉樹的層序遍歷
//層序遍歷public List<List<Character>> levelOrder(Node root){//創(chuàng)建一個(gè)二維數(shù)組保存每一層的元素List<List<Character>> list = new ArrayList<>();if(root == null){return list;}//臨時(shí)隊(duì)列Deque<Node> deque = new LinkedList<>();//頭節(jié)點(diǎn)放入隊(duì)列deque.offer(root);//隊(duì)列非空進(jìn)循環(huán)while(!deque.isEmpty()){int size = deque.size();List<Character> curList = new ArrayList<>();for (int i = 0; i < size; i++){Node x = deque.pop();//左子樹不為空,左子樹入隊(duì)列if(x.left != null){deque.offer(x.left);}//右子樹不為空,右子樹入隊(duì)列if(x.right != null){deque.offer(x.right);}//出棧的元素值存放在臨時(shí)數(shù)組里curList.add(x.val);}//出循環(huán)將臨時(shí)數(shù)組加入二維數(shù)組list.add(curList);}return list;}4.獲取樹中節(jié)點(diǎn)的個(gè)數(shù)
public int size(Node root){if(root == null){return 0;}return 1 + size(root.left) + size(root.right);}5.獲取葉子節(jié)點(diǎn)的個(gè)數(shù)
// 獲取葉子節(jié)點(diǎn)的個(gè)數(shù)int getLeafNodeCount(Node root){if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}6.獲取第K層節(jié)點(diǎn)的個(gè)數(shù)
// 獲取第K層節(jié)點(diǎn)的個(gè)數(shù)int getKLevelNodeCount(Node root,int k){if(root == null || k <= 0){return 0;}if(k == 1){return 1;}return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);}7.獲取二叉樹的高度
// 獲取二叉樹的高度int getHeight(Node root){if(root == null){return 0;}return 1 + Math.max(getHeight(root.left),getHeight(root.right));}8.檢測(cè)值為value的元素是否存在
// 檢測(cè)值為value的元素是否存在public boolean find(Node root, int val){if(root == null){return false;}if(root.val == val){return true;}return find(root.left,val) || find(root.right,val);}9.判斷一棵樹是不是完全二叉樹
// 判斷一棵樹是不是完全二叉樹boolean isCompleteTree(Node root){if(root == null){return true;}//隊(duì)列為空出循環(huán),兩個(gè)階段//1.所有都是度為2的節(jié)點(diǎn)//2.碰到第一個(gè)度為1的節(jié)點(diǎn),右節(jié)點(diǎn)直接false,左節(jié)點(diǎn)進(jìn)入第二階段//碰到第一個(gè)度為0的節(jié)點(diǎn),進(jìn)入第二階段//3。第二階段,都是葉子節(jié)點(diǎn),如果有不是葉子節(jié)點(diǎn),直接falseDeque<Node> deque = new LinkedList<>();deque.offer(root);boolean flag = true;while(!deque.isEmpty()){if(flag){Node x = deque.poll();if(x.left != null && x.right != null){deque.offer(x.left);deque.offer(x.right);}else if(x.right != null){return false;}else if(x.left != null){deque.offer(x.left);flag = false;}else {flag = false;}}else {Node x = deque.poll();if(x.left != null || x.right != null){return false;}}}return true;}